Jest to druga część tekstu z cyklu „Docisk, czyli jak projektować powierzchnie obciążone miejscowo” i dotyczy wymiarowania zbrojenia na poprzeczne siły rozciągające powstałe pod miejscem obciążenia.
W tej części pokażę Ci, jak wygląda rozkład obciążenia przyłożonego na niewielkiej powierzchni. Dowiesz się gdzie i dlaczego przy ściskaniu powstają dodatkowo siły rozciągające i jak sobie z nimi radzić. Na koniec nauczę Cię na przykładzie jak wymiarować zbrojenie w tego typu sytuacjach.
Pierwszą część tekstu dotyczącą określenia nośności na docisk powierzchni obciążonej miejscowo znajdziesz TUTAJ. Uwaga: Jeśli jeszcze nie zapoznałeś się z częścią 1, to najlepiej zrób to teraz, jeszcze przed zapoznaniem się z częścią drugą.
Zbrojenia na poprzeczne siły rozciągające
Generalnie w zjawisku docisku istnieją dwa przypadki położenia obciążenia miejscowego, które mogą wystąpić w konstrukcji:
- Obciążenie przyłożone w okolicy osi elementu,
- Obciążenie przyłożone poza osią elementu.
Pierwszy przypadek występuje wtedy, kiedy obciążenie zlokalizowane jest w pobliżu osi elementu i odległość obciążenia od krawędzi jest na tyle duża, że nie ma to wpływu na rozkład naprężeń pod przyłożonym obciążeniem. Takie obciążenie nazwiemy tutaj osiowym.
Drugi przypadek dotyczy obciążenia zlokalizowanego na tyle blisko krawędzi elementu, że zmienia on rozkład naprężeń. Tutaj mamy do czynienia z obciążeniem na mimośrodzie.
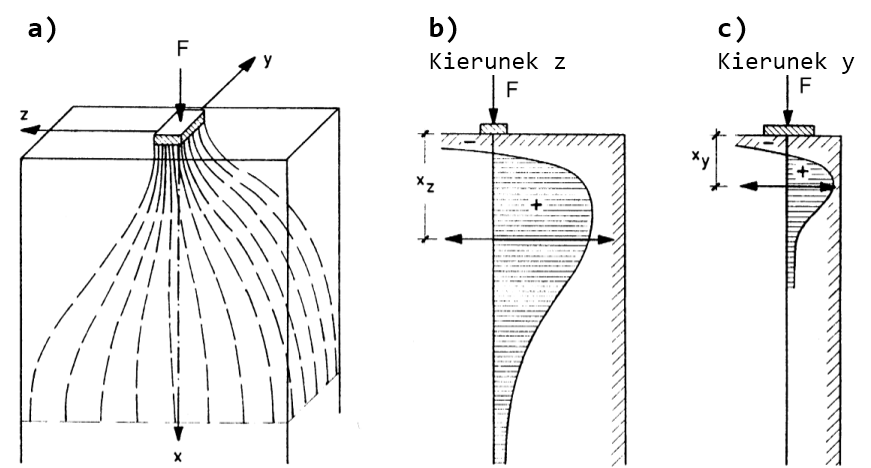
Rys. 1 Rozkład sił pod obciążeniem skupionym: a) sytuacja ogólna, b) obciążenie położone w okolicy osi elementu, c) obciążenie położone blisko krawędzi elementu [M. Rösler]
Każdy z tych przypadków może doprowadzić do rozłupania betonu na skutek poprzecznych sił rozciągających. Aby temu zapobiec, należy określić odpowiednie zbrojenie. Przejdźmy teraz do metod wyznaczania zbrojenia dla poszczególnych przypadków obciążenia.

Obciążenie w osi elementu
Rysunek 2 pokazuje sytuację, jaka występuje przy obciążeniu w osi elementu. Mamy tutaj wyraźnie rozwiniętą bryłę naprężeń rozciągających (zakreskowany trójkąt), która powinno przenieść zbrojenie poprzeczne.
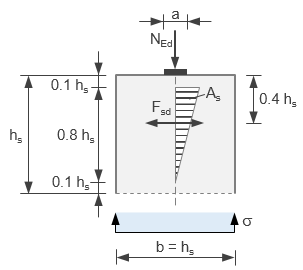
Rys. 2 Poprzeczne siły rozciągające – obciążenie w osi elementu
Zbrojenie zapobiegające rozłupaniu betonu pod obciążeniem przyłożonym w osi elementu wyznacza się ze wzorów:
Poprzeczna siła rozciągająca (rozłupująca):
![]()
Siła rozciągająca na krawędzi:
![]()
Zbrojenie wymagane:
![]()
Obciążenie w pobliżu krawędzi elementu (mimośród)
Rysunek 3 obrazuje sytuację, kiedy obciążenie zlokalizowane jest blisko krawędzi elementu. Tutaj może dojść do sytuacji, w której mimośród obciążenia będzie na tyle duży, że powstanie dodatkowa siła rozciągająca na krawędzi pionowej. Siłę tą oznaczoną jako ![]() przejmie zbrojenie krawędziowe.
przejmie zbrojenie krawędziowe.
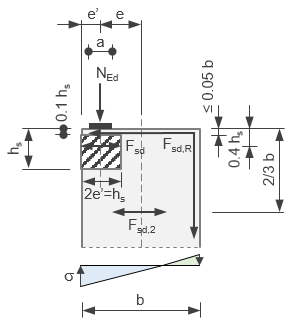
Rys. 3 Poprzeczne siły rozciągające – obciążenie poza poza osią elementu (w pobliżu krawędzi)
Poprzeczna siła rozciągająca (rozłupująca):
![]()
Siła rozciągająca na krawędzi:
![]()
Poprzeczna, drugorzędna siła rozciągająca:
![]()
Wymagane zbrojenie (dotyczy ![]() oraz
oraz ![]() ):
):
![Rendered by QuickLaTeX.com \[A_{s,req} = \frac{F_{sd,i}}{f_{yd}}\]](https://oprojektowaniu.pl/wp-content/ql-cache/quicklatex.com-7162dc95ae28a8a30f3afc40a780eaa2_l3.png)
Ograniczenie nośności na docisk w przypadku braku zbrojenia na siły poprzeczne
Tutaj muszę zrobić jedną ważną uwagę. Dotyczy ona sytuacji, kiedy nie zastosowano żadnego zbrojenia na poprzeczne siły rozciągające. Wtedy nośność na docisk ![]() (sposób określenia nośności opisałem tutaj) należy zredukować według poniższego wzoru:
(sposób określenia nośności opisałem tutaj) należy zredukować według poniższego wzoru:
![]()
Przykład obliczeniowy
Weźmy przykład z części 1 artykułu. Mamy zatem belkę opartą na ścianie (rys. 4). Wymiary przekroju poprzecznego belki: 25/45 cm, ściana o długości ![]() . Klasa betonu belki i ściany: C30/37. Reakcja do przeniesienia z belki na ścianę przez powierzchnię docisku wynosi
. Klasa betonu belki i ściany: C30/37. Reakcja do przeniesienia z belki na ścianę przez powierzchnię docisku wynosi ![]() .
.
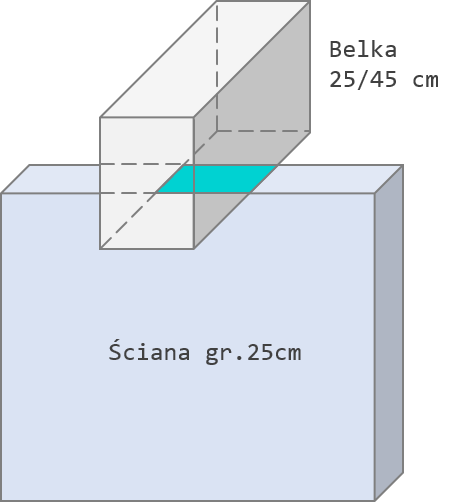
Rys. 4 Przykład obliczeniowy – podciąg oparty na ścianie
Obliczenia przeprowadzę tutaj dla dwóch przypadków: (1) obciążenie w osi elementu oraz (2) obciążenie w pobliżu krawędzi. Sprawdzenie nośności betonu na docisk ![]() znajdziesz tutaj.
znajdziesz tutaj.
(1) Obciążenie w osi elementu

Rys. 5 Poprzeczne siły rozciągające – obciążenie w osi elementu
![]()
Poprzeczna siła rozciągająca: ![]()
Wymagane zbrojenie:
![]()
Przyjęto zbrojenie:
- zbrojenie poprzeczne:

- zbrojenie krawędziowe:
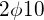 (przyjęto konstrukcyjnie,
(przyjęto konstrukcyjnie, 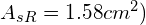
(2) Obciążenie w pobliżu krawędzi

Rys. 6 Poprzeczne siły rozciągające – obciążenie w pobliżu krawędzi elementu
![]()
![]()
![]()
Poprzeczna siła rozciągająca:
![]()
Siła rozciągająca na krawędzi:
![]()
Poprzeczna, drugorzędna siła rozciągająca:
![]()
Wymagane zbrojenie:
![]()
![]()
![]()
Przyjęto zbrojenie:
- zbrojenie poprzeczne:
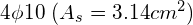
- zbrojenie krawędziowe:
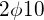 (przyjęto konstrukcyjnie,
(przyjęto konstrukcyjnie, 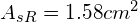 )
) - drugorzędne zbrojenie poprzeczne:
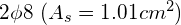
Uwaga końcowa: Uzupełnieniem tego tekstu jest część 1 artykułu dotycząca docisku betonu.
Źródła
- Eurokod 2: PN-EN 1992-1-1, Projektowanie konstrukcji z betonu. Część 1-1: Reguły ogólne i reguły dla budynków
- Fingerloos F., Hegger J., Zilch K., EUROCODE 2 für Deutschland – Kommentar, Ernst & Sohn / Beuth, 2016
- PN-B-03264:2012, Konstrukcje betonowe, żelbetowe i sprężone – Obliczenia statyczne i projektowanie
- Albert A. et al., Schneider – Bautabellen für Ingenieure, Bundesanzieger Verlag, 2016
- Vismann U. et al., Wendehorst Bautechnische Zahlentafeln, Springer / Beuth, 2015
- Rösler M., Teilflächebelastung, http://public.beuth-hochschule.de/~roeslerm/Skript/Teilflaechenbelastung.PDF [dostęp: 14.12.2018]
Z pozdrowieniami





Panie Łukaszu,
Skąd wziął się wzór na nośność na docisk w przypadku, kiedy nie zastosowano żadnego zbrojenia na poprzeczne siły rozciągające?
Odpowiedź znajdziesz w literaturze – zobacz źródła na końcu wpisu.
Jeśli odpowiedź znajduje się w źródłach niemieckojęzycznych, to osobiście raczej jej tam nie znajdę (ze względu na bardzo ograniczoną znajomości języka Goethego). W EC i PN nie znalazłem odpowiedzi. W źródłach rodzimych (w publikacjach prof. Starosolskiego) można znaleźć wzór na maksymalne naprężenia w pręcie (strut) przy rysach niewielkiej rozwartości, skierowanych ukośnie do naprężeń ściskających – Sigma Rd,max = 0,6 * fcd. Czy autorowi wzoru z artykułu przyświecała podobna filozofia?
Witam
Dlaczego w przykładzie obliczeniowym jest inna wartość Fsd dla siły osiowej i mimośrodowej? Wzór jak rozumiem jest taki sam a raz Fsd=169kN a potem 56kN.
Brawo Mateusz za czujność :) Wzór jest taki sam, tylko wartości hs w przykłądzie 1 i 2 są inne, odpowiednio 50 cm i 30 cm.
W przykładzie 2 wkradł się błąd – we wzorze na Fsd powinno być hs = 30 cm (poprawiłem już). Uzupełniłem też wzór Fsd,R o człon 1/6.
Witam,
Czy jest jakieś ciekawe podejście do tematu oparcia ściany na prostopadłej ścianie przez strop. Dla przykładu ściana 18cm opiera się poprzecznie na ścianie 18cm. Pomijając udział stropu, pole docisku będzie równe 18cm * 18cm=324cm2. Dla betonu C30/37 takie połączenie powinno przenieść 324cm2 * 2 kN/cm2= 648kN. W modelu powłokowym mogę odczytać tylko naprężenie i ewentualnie dozbrajać. I tu jest pierwszy problem, że nie mogę wyznaczyć konkretnej siły pionowej. Czy prowadził Pan jakieś analizy takich połączeń? Bo ta nośność wydaje się mocno zaniżona i wpływ stropu intuicyjnie może kilkukrotnie podnosić nośność. Zdarza się czasami pogrubiać w takich połączeniach strop np. do 50cm i próbować jakoś ręcznie rozkładać te siły w tym pod kątem 45stopni i udowadniać nośność. Ale takie podejście jest nie za bardzo jest umocowane w jakiś dokładniejszych analizach. Temat jest dość powszechny w budownictwie kubaturowym, więc rozwinięcie go mogłoby być bardzo interesujące.
W przypadku niewystarczającej nośności samego betonu można dodać zbrojenie pionowe. Zbrojenie to zwiększa nośność tej powierzchni. Szczegóły znajdziesz w pierwszej części artykułu dotyczącego docisku. Link TUTAJ.
Jeśli chodzi o odczyt miarodajnej siły („reakcji”) przekazywanej ze ściany górnej na dolną, to tutaj pojawia się ograniczenie metody obliczeniowej MES. Naprężenia w tym miejscu nie są miarodajne – wystąpi typowa osobliwość MESu… Sam temat jest ciekawy i wymaga zastanowienia.