Wpis ten jest kontynuacją wpisu poprzedniego dotyczącego obciążeń zmiennych na stropach płytowo-słupowych. Będzie to uzupełnienie analizy rozkładu obciążeń zmiennych o dwie alternatywne metody.

Za cel postawiłem sobie zaproponowanie metody, która po pierwsze: będzie mniej pracochłonna od przedstawionych poprzednio metod tradycyjnych, i po drugie: jej dokładność będzie zbliżona do tej otrzymanej z rozkładu obciążeń wg schematu niezależnego.

Poprzedni post wyszedł trochę długi. Ale była to konieczność z racji samego tematu. Obiecuję, że ten będzie krótszy :)

Model obliczeniowy stropu płytowo-słupowego

Model obliczeniowy pozostaje bez zmian – szczegóły znajdziecie w poprzednim poście.

Alternatywne metody rozkładu obciążeń zmiennych

W celu ograniczenia pracochłonności modelowania obciążeń zmiennych i wykorzystując zalety schematu niezależnego, zaproponowałem alternatywne schematy rozkładu obciążenia zmiennego. Polegają one na wielokrotnym rozkładzie obciążeń zmiennych w ramach tego samego schematu obciążenia zachowując założony dopuszczalny poziom odchyłek (przyjąłem – jak poprzednio – błąd na poziomie 5%). Taka alternatywa – być może niektórym znana – ma za zadanie usprawnić modelowanie obciążeń zmiennych zwłaszcza w ustrojach o znacznej liczbie pól przewidzianych do niezależnego obciążenia. W rezultacie liczba schematów obciążeń ulegnie wyraźnie zmniejszeniu. Przeanalizuję dwa schematy:

1. Schemat obciążenia co 2. pole – polega na rozdzieleniu obszarów obciążonych jednym obszarem nieobciążonym dla obu kierunków. Redukcja liczby schematów do 4, niezależnie od liczby pól (rys. 1),
2. Schemat obciążenia co 3. pole – rozdzielenie obszarów obciążonych dwoma obszarami nieobciążonymi dla obu kierunków. Redukcja liczby schematów do 9, niezależnie od liczby pól (rys. 2).

Rys. 1 Wielokrotny schemat obciążeń niezależnych – obciążenie co drugie pole (poszczególne kolory odpowiadają pojedynczemu przypadkowi obciążenia)

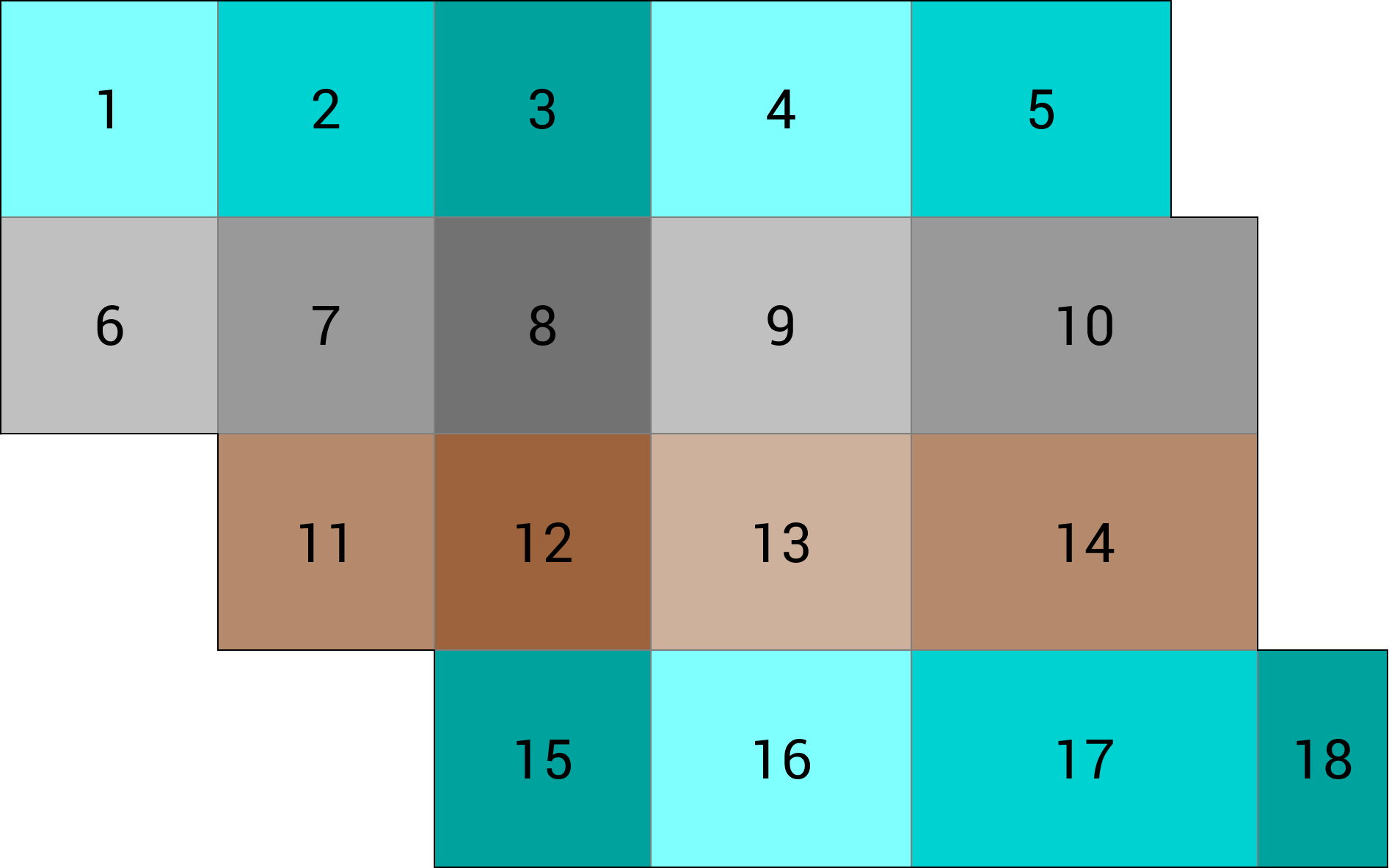
Rys. 2 Wielokrotny schemat obciążeń niezależnych – obciążenie co trzecie pole (poszczególne kolory odpowiadają pojedynczemu przypadkowi obciążenia)

Poniższe tabele 1 i 2 prezentują wyniki obliczeń dla alternatywnych schematów rozkładu obciążeń zmiennych i ich różnice w odniesieniu do rozwiązania dokładnego uzyskanego z powierzchni wpływu. Wartości procentowe (%) przedstawiają względną różnicę błędu, gdzie znak „-” (minus) oznacza niedomiar.

Obciążenie co 2. pole

Tab. 1a Schemat obciążeń i wyniki momentów zginających mx dla alternatywnego rozkładu obciążeń zmiennych co 2. pole

Rozpatrywane miejsce	Schemat obciążenia	Moment mx [kNm/m]
a) przęsło wewnętrzne		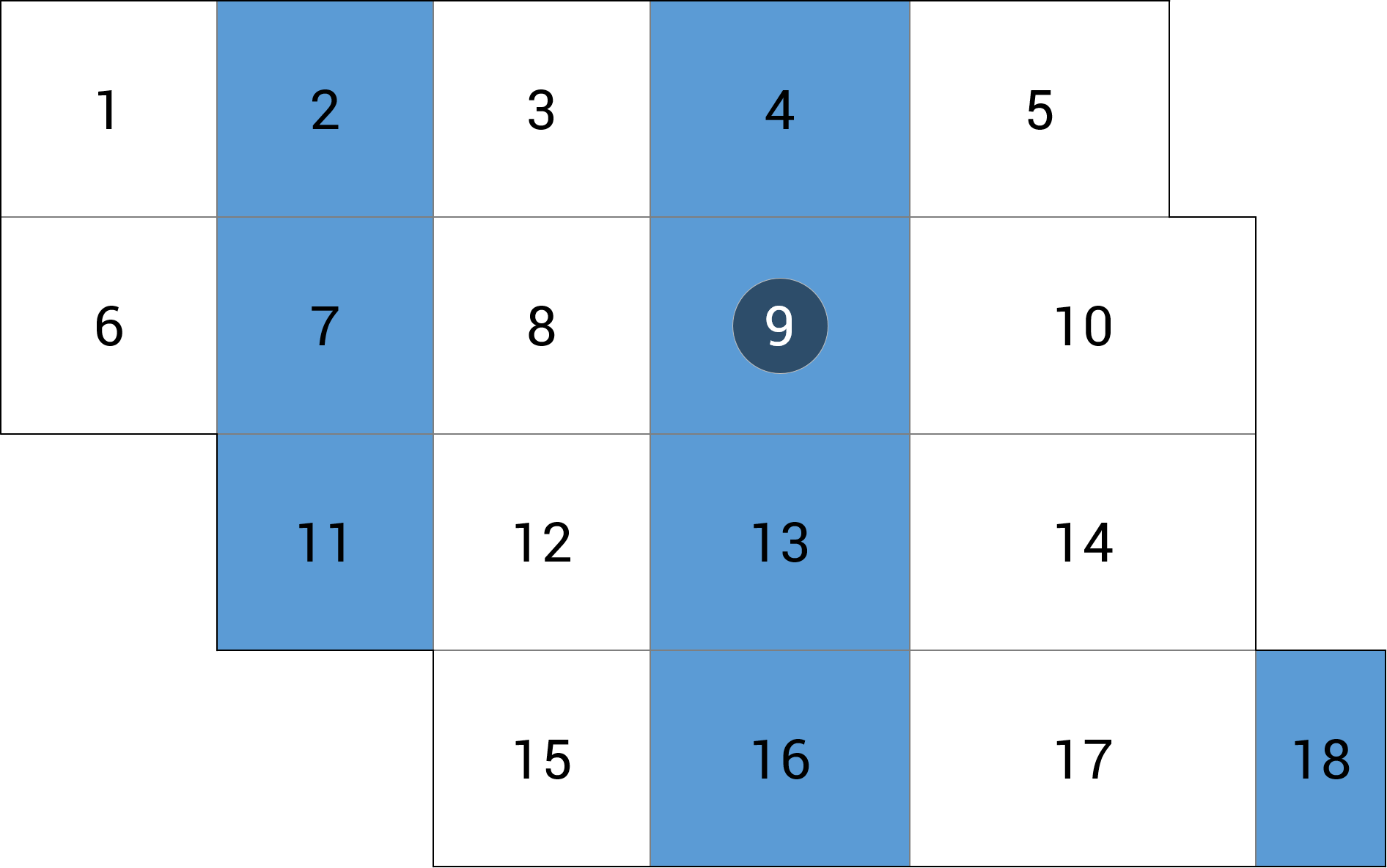+12.53 (0.8%)
b) przęsło skrajne		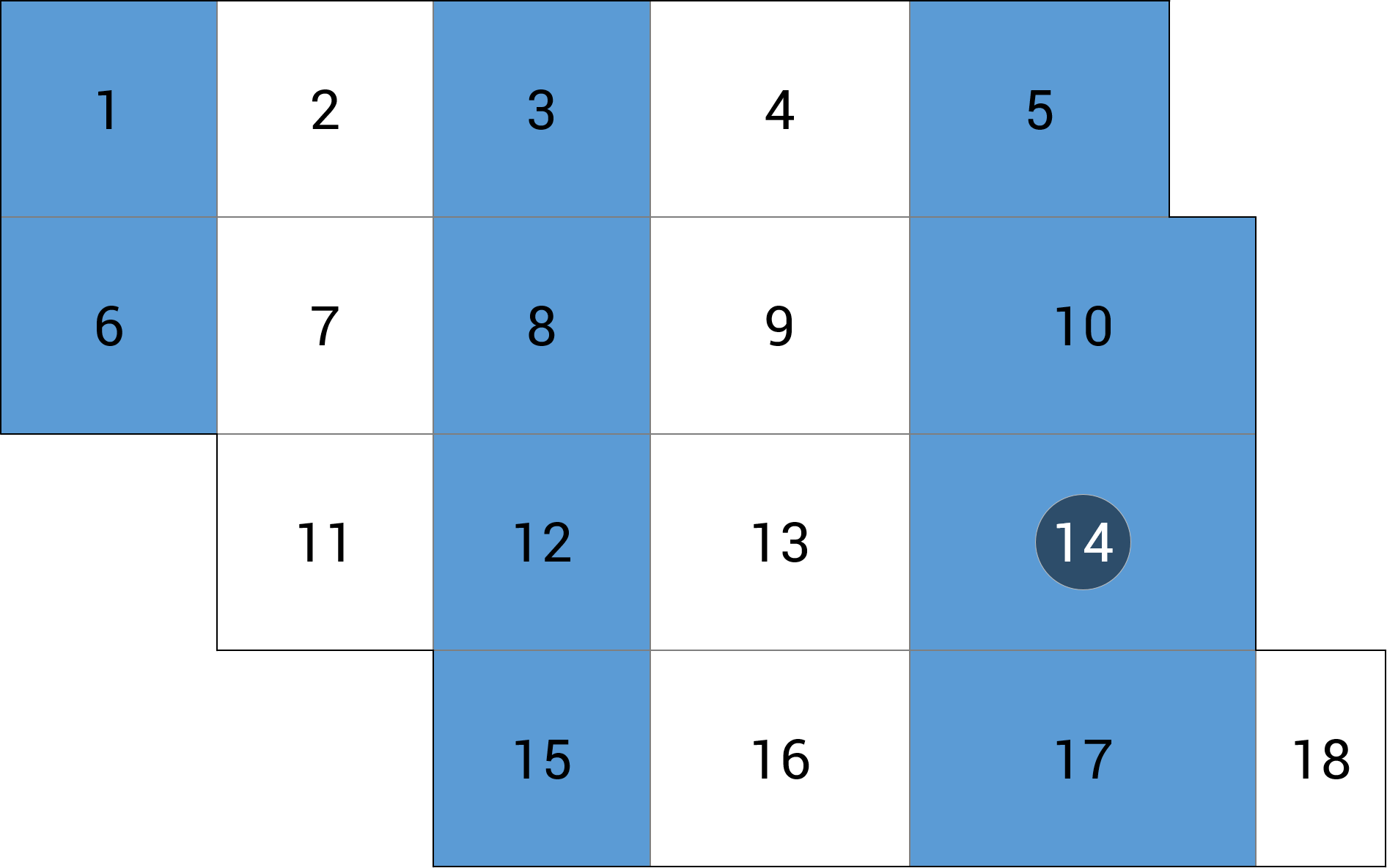+21.59 (-1.0%)
c) linia podpór		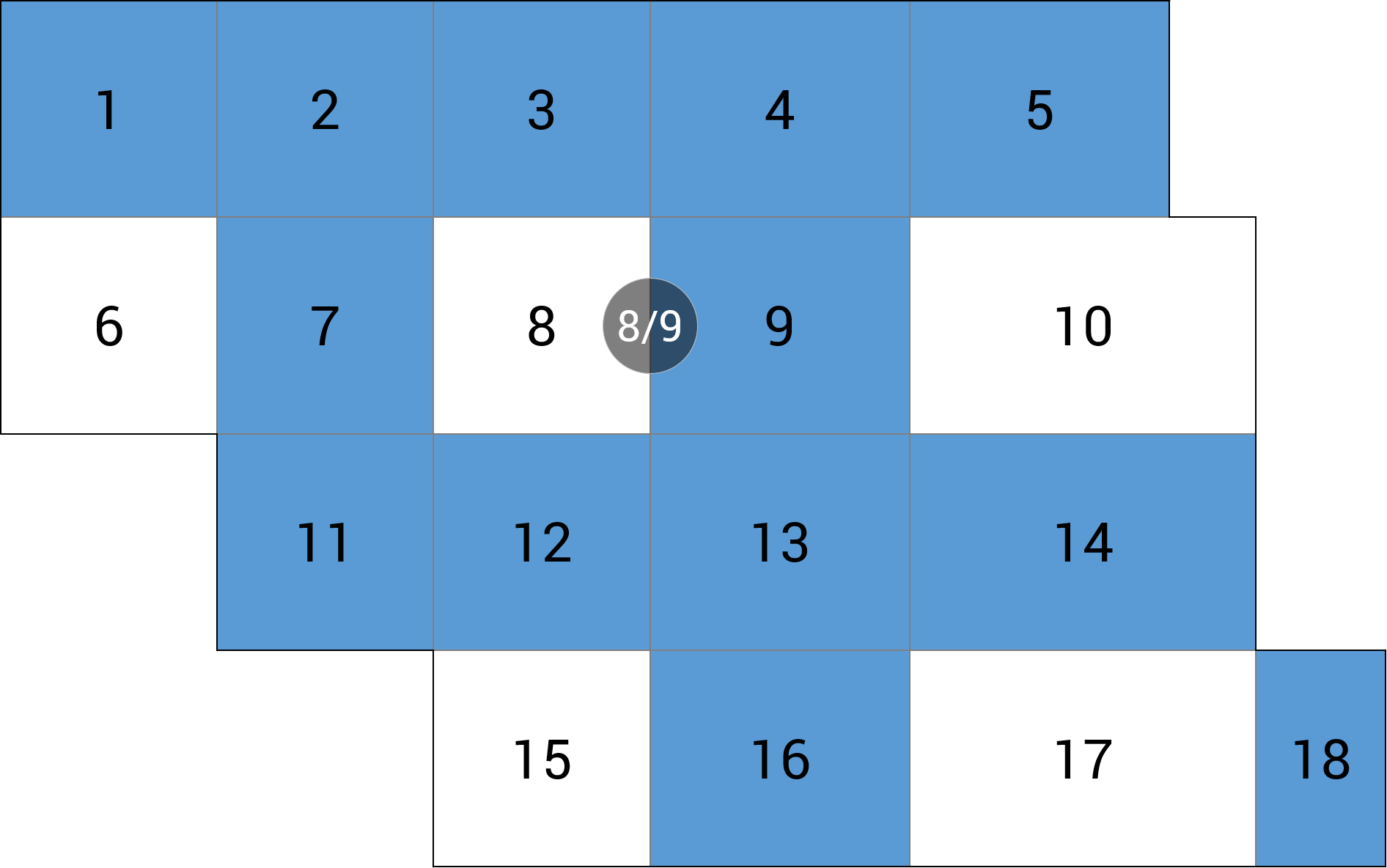-4.19 (-49.7%)
d) podpora		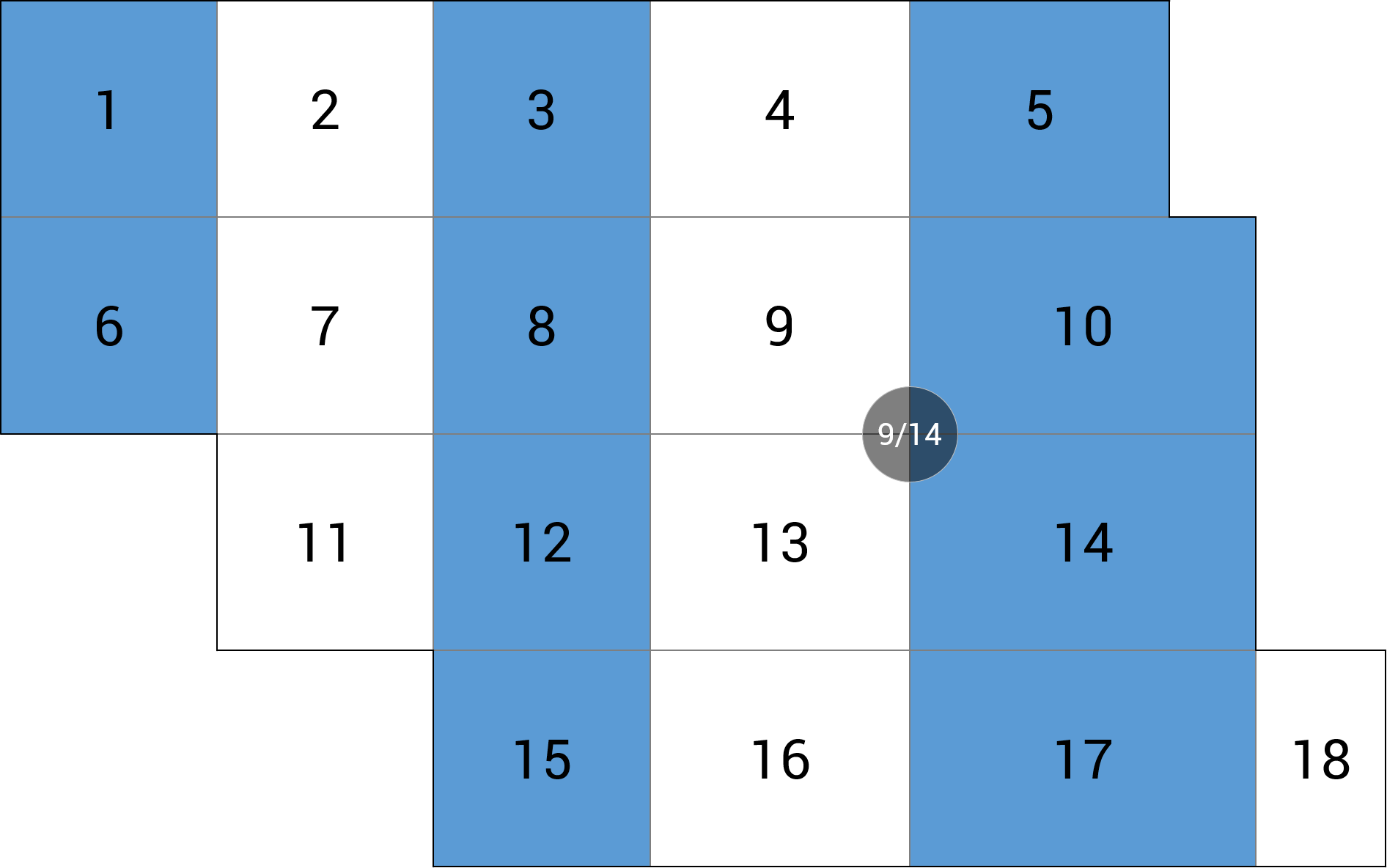MY = -25.86 kNm (0.9%)

Tab. 1b Schemat obciążeń i wyniki ugięć dla alternatywnego rozkładu obciążeń zmiennych co 2. pole

Rozpatrywane miejsce	Schemat obciążenia	Ugięcie [mm]
a) przęsło wewnętrzne	(Jak dla mx)	-2.11 (-4.5%)
b) przęsło skrajne	(Jak dla mx)	-5.81 (-0.7%)
c) linia podpór		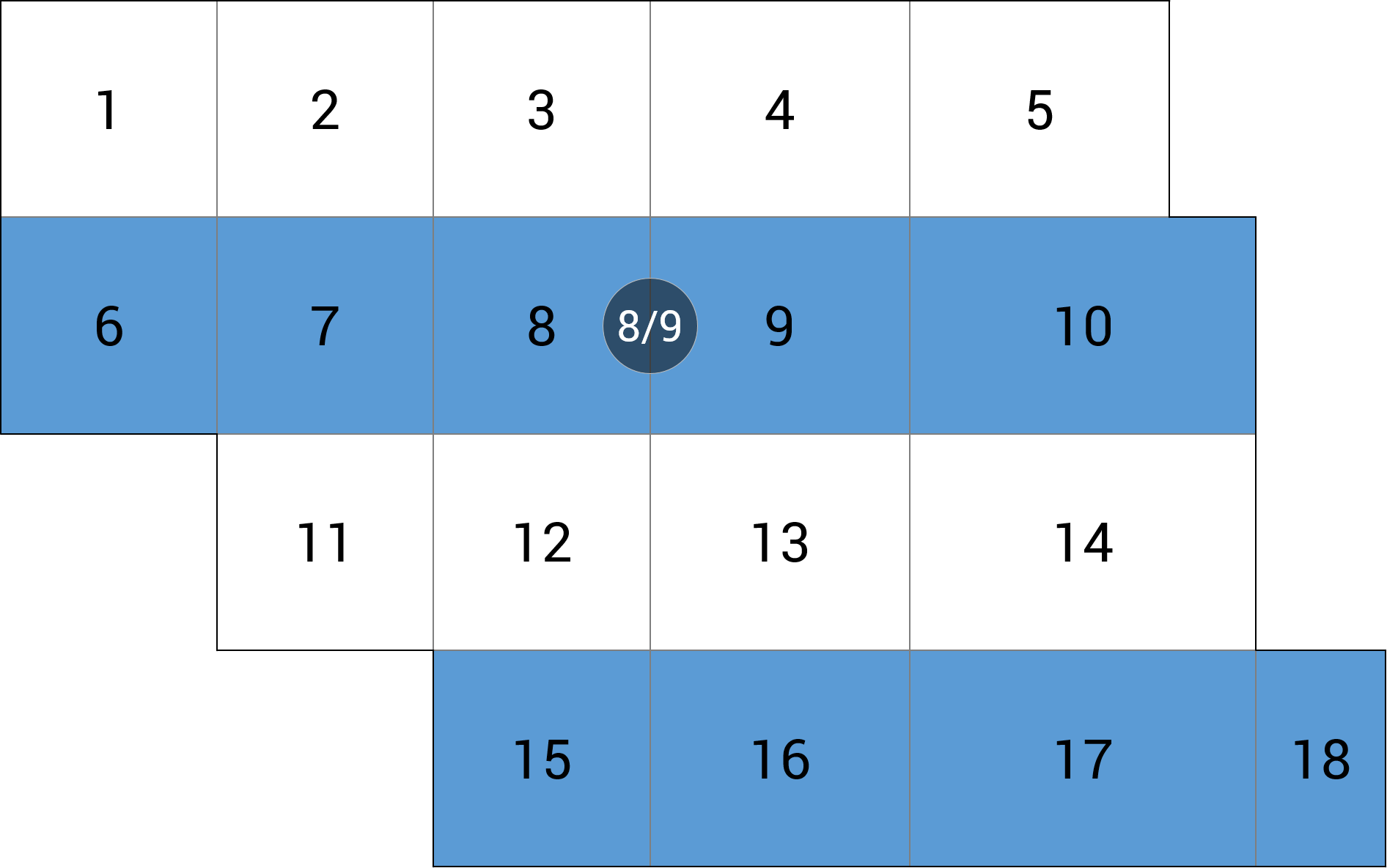-1.14 (-6.6%)
d) podpora		RZ = +185.1 kN (-11.5%)

Obciążenie co 3. pole

Tab. 2a Schemat obciążeń i wyniki momentów zginających mx dla alternatywnego rozkładu obciążeń zmiennych co 3. pole

Rozpatrywane miejsce	Schemat obciążenia	Moment mx [kNm/m]
a) przęsło wewnętrzne		+12.20 (-1.9%)
b) przęsło skrajne		+21.51 (-1.3%)
c) linia podpór		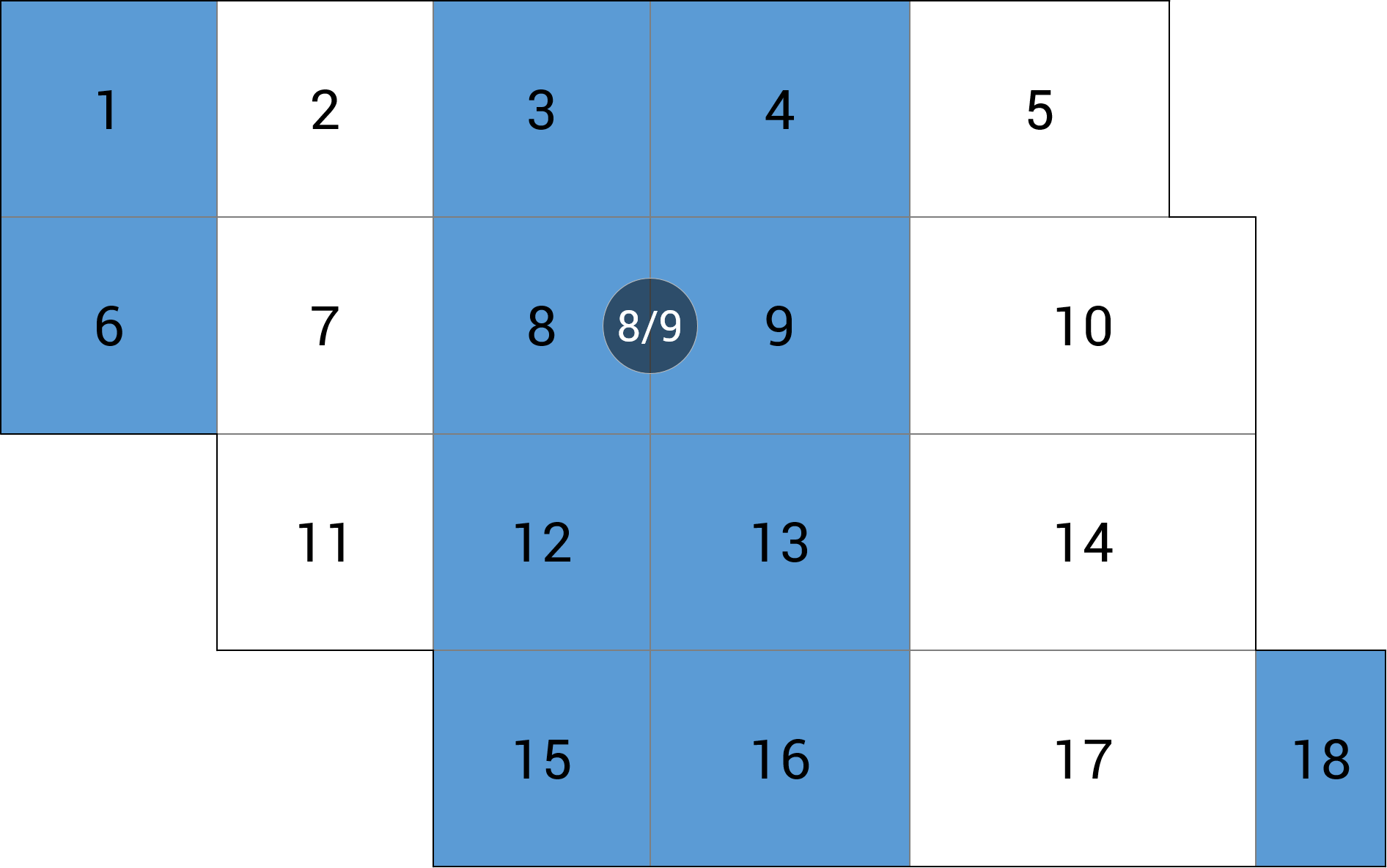-5.59 (-32.9%)
d) podpora		MY = -25.25 kNm (-1.5%)

Tab. 2b Schemat obciążeń i wyniki ugięć dla alternatywnego rozkładu obciążeń zmiennych co 3. pole

Rozpatrywane miejsce	Schemat obciążenia	Ugięcie [mm]
a) przęsło wewnętrzne	(Jak dla mx)	-2.07 (-6.3%)
b) przęsło skrajne		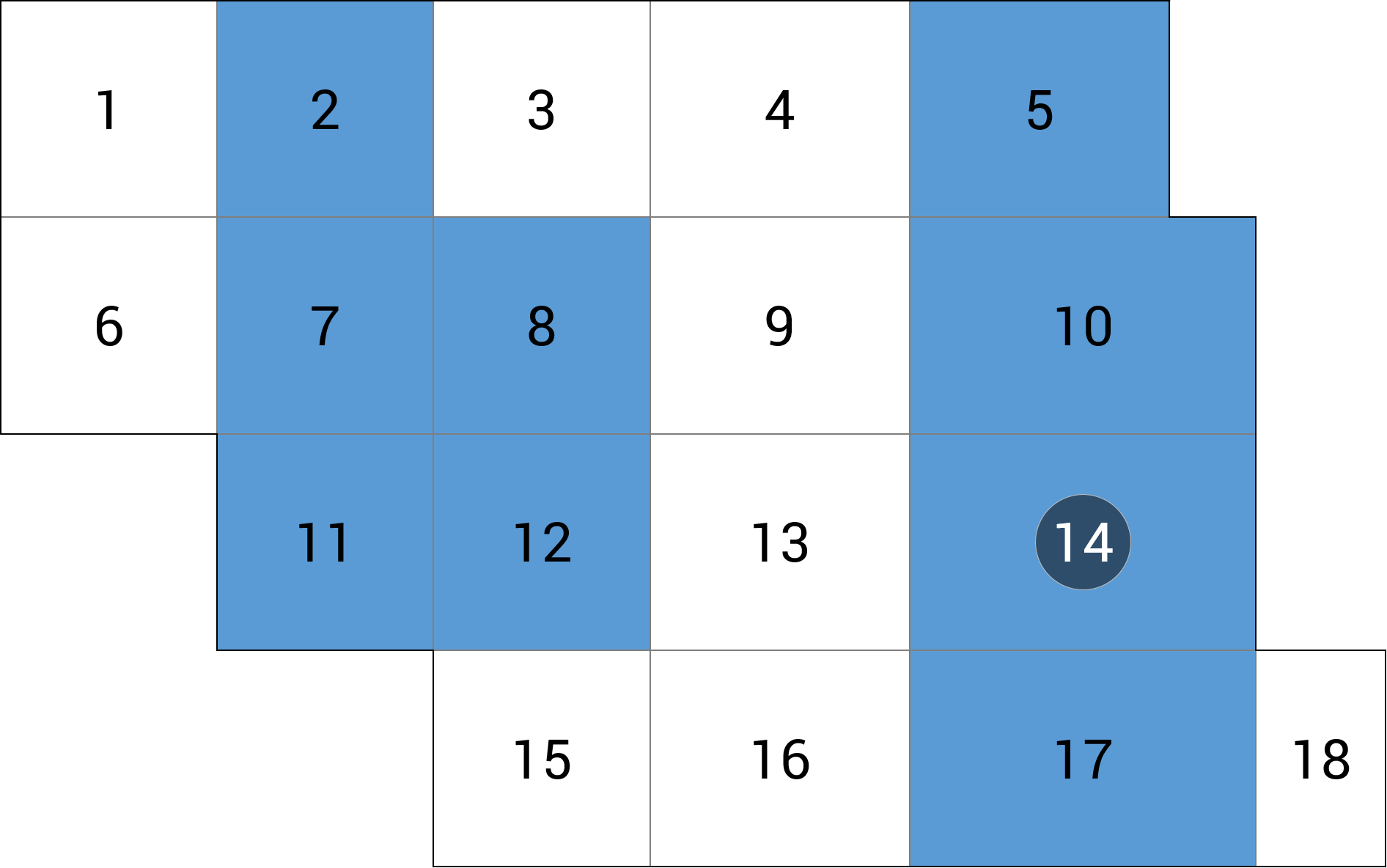-5.76 (-1.5%)
c) linia podpór		-1.13 (-7.4%)
d) podpora		RZ = +206.4 kN (-1.3%)

Zestawienie wyników schematów alternatywnych

Spójrzmy teraz na wyniki zestawione razem w tabli nr 3 i oceńmy ich dokładność względem rozwiązania dokładnego. Dodatkowo, powtórzyłem tutaj wyniki uzyskane dla schematu niezależnego – będzie nam łatwiej zorientować się jak miarodajne są schematy alternatywne. Dorzucę też pod nimi kilka zdań komentarza.

Tab. 3a Zestawienie odchyłek momentów zginających mx dla alternatywnych schematów rozkładu obciążeń zmiennych (błąd w %)

Schemat obciążeń	a) przęsło wewnętrzne	b) przęsło skrajne	c) linia podpór	d) podpora
Schemat niezależny	+0.8	-0.6	-31.7	+0.9
Schemat obciążeń co 2. pole	+0.8	-1.0	-49.7	+0.9
Schemat obciążeń co 3. pole	-1.9	-1.3	-32.9	-1.5

Tab. 3b Zestawienie odchyłek ugięć dla alternatywnych schematów rozkładu obciążeń zmiennych (błąd w %)

Schemat obciążeń	a) przęsło wewnętrzne	b) przęsło skrajne	c) linia podpór	d) podpora (RZ)
Schemat niezależny	-4.5	-0.7	-4.9	-1.2
Schemat obciążeń co 2. pole	-4.5	-0.7	-6.6	-11.5
Schemat obciążeń co 3. pole	-6.3	-1.5	-7.4	-1.3

Wielokrotny schemat obciążeń zmiennych co 2. pole daje dla stref przęsłowych (a i b) wyniki zadowalające dla momentów mx i ugięć, tj. z akceptowalnym błędem poniżej 5%. Są to wartości bliskie tym otrzymanym dla powierzchni wpływu jak i dla schematów niezależnych.

Jeśli chodzi natomiast o wyniki w linii podpór, to wartości momentów zginających odbiegają od wartości miarodajnych w tym obszarze. Błąd niedoszacowania dla mx wynosi ok. 50%; błąd ugięć wykazuje również niedomiar, jednak nie jest tak istotny (poniżej 7%).

Z kolei moment podporowy jest bliski wartości uzyskanej w metodzie dokładnej (błąd poniżej 1%). Inaczej jest już z reakcją podporową, której wartość obarczona jest błędem blisko 12%, dodatkowo jest to błąd niedomiaru.

Taki rozrzut wyników, zwłaszcza, że są to w większości błędy niedomiaru, ogranicza stosowanie tego schematu na poziomie założonej dokładności jedynie do stref przęsłowych.

Schemat rozkładu obciążeń zmiennych co 3. pole daje nam zazwyczaj wyniki zadowalające w odniesieniu do rozwiązania dokładnego i bliskie wartościom ze schematu niezależnego. Wyniki w obszarach przęsłowych wewnętrznym i skrajnym dają nam dokładność obliczeń na poziomie poniżej 2%. Wyjątek stanowi jedynie wartość ugięcia w prześle wewnętrznym, gdzie błąd niedomiaru jest na poziomie 6%, co ze względu m.in. na lokalizację możemy uznać mimo wszystko za wynik zupełnie zadowalający – w okolicy 5%.

Istotniejsze różnice w wynikach względem rozwiązania na podstawie powierzchni wpływu występują w obszarze w linii podpór. Błąd względny wartości momentu zginającego jest na poziomie 33%. Przypomnę, że błąd tej wartości w schemacie obciążenia co 2. pole wyniósł 50%, natomiast w odniesieniu do schematu obciążeń niezależnych błąd ten jest podobny (różnica pomiędzy tymi dwoma schematami wynosi ok. 1%). Błąd ugięcia w tym miejscu wynosi ok. 7% niedomiaru, co ze względu na lokalizację uznać możemy – jak wyżej – za wynik zadowalający.

Wartości momentu jak i reakcji podporowej pokrywają się z rozwiązaniem dokładnym na poziomie błędu poniżej 2%.

Porównując oba alternatywne schematy rozkładu obciążeń: co 2. jak i co 3. pole otrzymujemy wyniki zadowalające w strefach przęsłowych. Jednak w pozostałych analizowanych obszarach są dwie istotne różnice.

Pierwszą z nich jest dokładność wyników w linii podpór. Tak jak błąd ugięć dla obu schematów jest podobny (niedomiar ok. 7%), tak różnica błędu w wartościach momentów zginających jest tutaj istotna (powyżej 30%). Warto podkreślić, że wynik dla momentu mx dla schematu co 3. pole jest obarczony niemal jednakowym błędem co wynik otrzymany ze schematu niezależnego.

Drugą różnicą pomiędzy alternatywnymi schematami jest niedoszacowanie reakcji podporowej w schemacie co 2. pole o ok. 12%, w przeciwieństwie do schematu co 3. pole, gdzie błąd reakcji jest na poziomie poniżej 2% względem rozwiązania dokładnego.

Wnioski

Pamiętacie wnioski z poprzedniego wpisu? Przydadzą się nam teraz. Przypomnę wniosek końcowy: spośród pięciu przeanalizowanych typowych schematów rozkładu obciążeń zmiennych, najbardziej miarodajnym jest schemat niezależny. Mankamentem tego rozwiązania jest jednak jego pracochłonność przy stropach o większej liczbie pól (np. powyżej 10).

Wielokrotne schematy obciążeń niezależnych o rozkładzie co 2. lub co 3. pole wydają się być skutecznym sposobem rozkładu obciążeń zmiennych a dzięki swojej prostocie redukują istotnie nakład pracy. Są to sposoby, których wyniki obliczeń w większości nie odbiegają znacząco od rozwiązania dokładnego i są zbliżone do wyników ze schematu niezależnego.

Schemat rozkładu obciążeń co 2. pole można uznać za poprawny przede wszystkim w odniesieniu do obszarów przęsłowych (błąd poniżej 5%). W linii podpór wykazuje on już większe błędy niedomiaru w wynikach obliczeń (50% dla momentu zginającego). Podobnie jest w strefie podporowej (reakcja podporowa z niedomiarem ok. 12%). Stwarza to ryzyko zmniejszenia zapasu bezpieczeństwa w obliczeniach stropu, jak też później podpór. Mimo swojej prostoty i ograniczenia liczby schematów obciążeń zmiennych do 4, wymaga ostrożności w stosowaniu.

Schemat rozkładu obciążeń co 3. pole jest sensownym kompromisem pomiędzy dokładnością wyników względem rozwiązania dokładnego a nakładem włożonej pracy. W odróżnieniu od schematu niezależnego generuje maksymalnie do 9 przypadków obciążenia zmiennego niezależnie od liczby pól obciążenia. To znacznie zmniejsza pracochłonność pracy przy modelowaniu, jednocześnie nie tracąc przy tym znacząco na dokładności wyników. Wartości uzyskane w przęsłach i nad podporami pokrywają się z rozwiązaniem dokładnym w graniach błędu ok. 5% (6% dla ugięć przęsła wewnętrznego). Natomiast błąd względny w wartości momentu zginającego w linii podpór wynosi ok. 33% w stosunku do rozwiązania dokładnego i jest o tyle akceptowalny, że pokrywa się z dokładnością schematu niezależnego (różnica między nimi ok. 1%).

Dodatkowo, o czym pisałem wcześniej przy okazji schemat niezależnego, różnice między rozwiązaniem dokładnym a schematem obciążenia co 3. pole, zacierają się z racji wpływu składowej od obciążeń stałych czy wielkości powierzchni stropu.

Podsumowanie

Podsumowując temat rozkładu obciążeń zmiennych na stropach płytowo-słupowych – uwzględniając tutaj również wyniki analiz z poprzedniego wpisu dotyczącego typowych schematów – można sprowadzić to do dwóch zasadniczych wniosków. Zatem jedziemy :)

1. Najdokładniejszym sposobem rozkładu obciążeń zmiennych na stropie płytowo-słupowym jest schemat obciążeń niezależnych. W przypadku niewielkiej liczby pól obciążeń (założono do 10 pól) jest on efektywny i generuje miarodajne wyniki momentów zginających, ugięć i reakcji podporowych w odniesieniu do rozwiązania dokładnego opartego na powierzchniach wpływu.
2. W przypadku większej liczby pól obciążeń (powyżej 10) zaleca się stosować alternatywny sposób rozkładu obciążeń zmiennych co 3. pole. Sposób ten zapewnia zbliżone wyniki do schematu niezależnego jednocześnie redukując przy tym liczbę przypadków obciążeń zmiennych do 9 niezależnie od liczby pól.

Jakie wy macie wnioski? Było tego sporo, ale udało nam się temat rozpracować oraz wskazać dwie konkretne i bezpieczne metody rozkładu obciążeń zmiennych (schemat obciążeń niezależnych oraz schemat rozkładu obciążeń co 3. pole). Jeśli chcielibyście coś dodać, to chętnie się tego dowiem – piszcie :)

Wpisy z cyklu „Rozkład obciążeń zmiennych„:

1. Powierzchnie wpływu,
2. Strop płytowo-słupowy,
3. Strop płytowo-słupowy – metody alternatywne,
4. Strop płytowo-belkowy,
5. Strop oparty na ścianach (w opracowaniu).

Źródła

• Starosolski W., Aneks do: Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, na prawach rękopisu, Pro-Soft, Gliwice 2007,
• Starosolski W., Komputerowe modelowanie betonowych ustrojów inżynierskich. Wybrane zagadnienia, t.1 i 2, Wyd. Politechniki Śląskiej, Gliwice 2009,
• Starosolski W., O rozmieszczeniu obciążeń zmiennych w stropach krzyżowo zbrojonych i płytowo-słupowych, Inżynieria i Budownictwo, nr 4/2008,
• Starosloski W., Projektowanie płytowo-słupowych ustrojów żelbetowych i sprężonych wg Euro-Norm, PRO-SOFT, Gliwice 2010,
• Starosolski W., Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, Wyd. Politechniki Śląskiej, Gliwice 2003,
• Zdanowicz Ł., Praca magisterska: Analiza obliczeniowa i projekt konstrukcji wielokondygnacyjnego budynku o ustroju płytowo-słupowym, Kraków 2010.