Projektujemy, optymalizujemy i odchudzamy konstrukcje, żyłujemy zbrojenie w betonie itd. Ale czy to wystarczy? A co z obciążeniami, a dokładnie: co z obciążeniami zmiennymi? Czy rozkładamy je właściwie? Jak określić który ze sposobów rozłożenia obciążeń zmiennych na stropie jest tym właściwym? Który z nich jest najefektywniejszy, czyli wymaga minimalnego wysiłku i daje jednocześnie miarodajne wyniki sił wewnętrznych i ugięć? Czy istnieje jakiś uniwersalny sposób takiego rozkładu obciążeń, czy jest ich kilka? Czy musimy wybierać taki sposób w zależności od typu konstrukcji? Na te pytania postaram się odpowiedzieć w tym cyklu wpisów. Dalej – znajdziemy rozwiązanie!
Zacznę trochę sucho, bo od tego, co mówią normy. Sprawą zasadniczą przy projektowaniu konstrukcji jest problem korelacji model obliczeniowy – rzeczywistość. Model obliczeniowy – idąc za Eurokodem 0 – jest idealizacją ustroju konstrukcyjnego, stosowaną w celu analizy, wymiarowania i weryfikacji, a „siły wewnętrzne w konstrukcji oblicza się przyjmując modele obliczeniowe odwzorujące warunki pracy konstrukcji” (cytat wyjęty z poprzedniej normy żelbetowej, PN02). Jest to problem uniwersalny bez względu na zmiany norm i podstawowy – dotyczy wszystkich konstrukcji.
W tej części pokażę wam jak dokładnie określić sposób rozkładu obciążeń zmiennych na stropach żelbetowych. Podam też sposób jak określić, które pola stropu należy obciążyć w celu uzyskania ekstremalnych wartości momentów zginających, ugięć czy reakcji podporowych. Jest to kluczowe pytanie rzutujące na wszystkie kolejne wyniki obliczeń statycznych.
Naszym celem jest uzyskanie możliwie najbardziej niekorzystnego schematu rozkładu obciążeń zmiennych, wywołującego ekstremalne ugięcia i siły wewnętrzne. Wartości ekstremalne będą tutaj najczęściej rozumiane jako wartości maksymalne co do wartości bezwzględnej z zachowanie znaku (określenia będą używane zamiennie).
Trochę teorii
Żeby odpowiedzieć na postawione wyżej pytania, musimy sięgnąć do naszej pamięci i przypomnieć sobie pewną funkcję – powierzchnię wpływu. Być może lepiej znana jest jej inna odmiana – linia wpływu. Różnica pomiędzy linią a powierzchnią wpływu generalnie jest taka, że ta pierwsza dotyczy elementów belkowych (prętów), natomiast ta druga płyt (elementów powierzchniowych). Zasada działania jest podobna.
Jest kilka sposobów określania powierzchni wpływu. Niektóre programy obliczeniowe mają takie funkcje wbudowane. Tutaj podam wam skuteczny sposób na określenie powierzchni wpływu dla różnych wielkości (jak ugięcie, moment zginający czy reakcja podpora) korzystając z podstawowych funkcji jaką mają typowe programy obliczeniowe, których używamy na co dzień. W tym przykładzie wykorzystałem program ABC Płyta autorstwa dra inż. K. Grajka.
Powierzchnie wpływu możemy otrzymać za pomocą metody kinematycznej dla układów Clapeyrona wykorzystując twierdzenie Maxwella-Bettiego. Wybaczcie mi tutaj te nazwiska, ale chodzi o zasadę prac wirtualnych. Upraszczając, wymienione twierdzenia dotyczą układów, w których występujące odkształcenia są proporcjonalne do odpowiadających im sił (Clapeyron) oraz o to, że dla tego samego układu istnieje ścisła zależność pomiędzy przyłożonymi oddziaływaniami a efektami tych oddziaływania w różnych punktach (Maxwell-Betti). Metodę kinematyczną można z powodzeniem stosować dla większości naszych modeli. Zainteresowanych odsyłam do książki Wytrzymałość materiałów, Jastrzębski, Mutermilch, Orłowski (źródła podałem na dole). Sam też zajmowałem się tym zagadnieniem w części teoretycznej mojej pracy magisterskiej.
Jak wyznaczyć powierzchnie wpływu?
Aby wyznaczyć powierzchnie wpływu należy przeprowadzić typowe obliczenia naszego stropu z kilkoma modyfikacjami. Analizę przeprowadziłem dla maksymalnych przemieszczeń, momentów zginających jak i reakcji podporowych w wybranych miejscach stropu. Metoda ta polega na dobraniu w analizowanym punkcie płyty odpowiednich przemieszczeń (przemieszczeń w pionie lub obrotów – odpowiednio dla ugięć i momentów zginających), na podstawie których – po otrzymaniu obrazu przemieszczeń płyty – można odczytać obszary, gdzie należy założyć obciążenia dla uzyskania największych wartości sił wewnętrznych lub ugięć dla tego punktu.
Dla przykładu, do określenia obszarów płyty, które należy obciążyć dla uzyskania największego ugięcia w analizowanym punkcie (np. w środku przęsła), należy w punkcie tym zadać siłę skupioną o kierunku zgodnym z oczekiwanym przemieszczeniem (tutaj „w dół” – w kierunku osi Z; wartość obciążenia nie ma tutaj większego znaczenia), por. rys. 1. Obszary płyty o znaku przemieszczeń zgodnym z kierunkiem działania siły, będą obszarami, obciążenie których spowoduje największe wartości przemieszczeń w analizowanym punkcie (tutaj w przęśle).
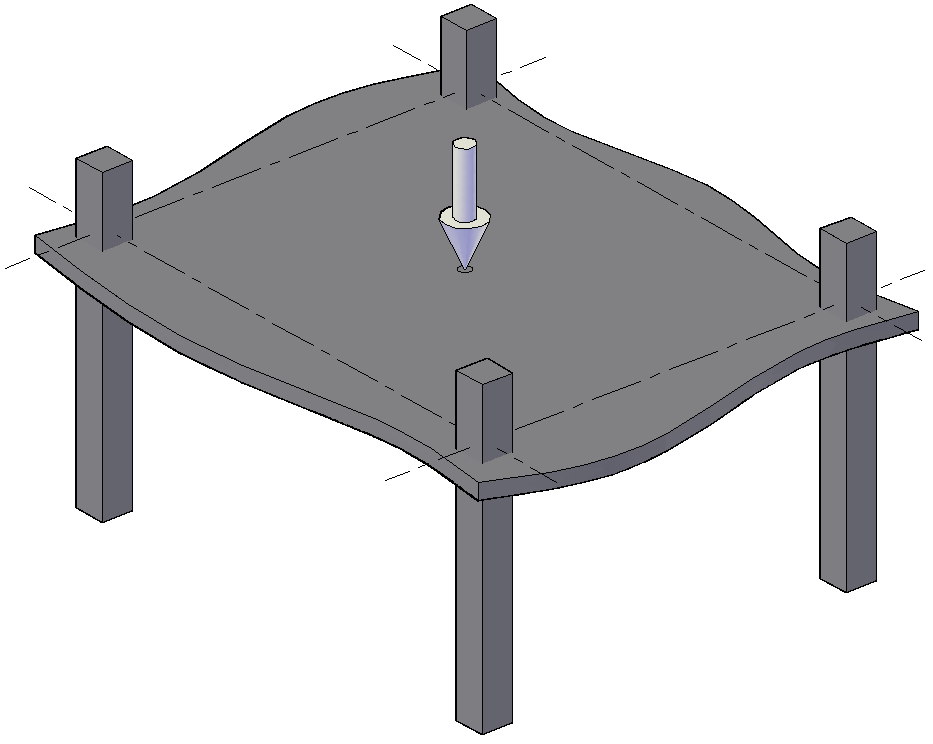
Rys. 1 Schemat obciążenia do wyznaczenia powierzchni wpływu dla maksymalnych przemieszczeń przęsła
Analogicznie otrzymamy powierzchnie wpływu dla momentów zginających w wybranym punkcie (por. rys. 2 poniżej). Zamiast siły pionowej zakłada się parę momentów o przeciwnych zwrotach na krawędzi elementu skończonego stanowiącego quasi-przegub (10-20-krotne pocienienie grubości płyty).
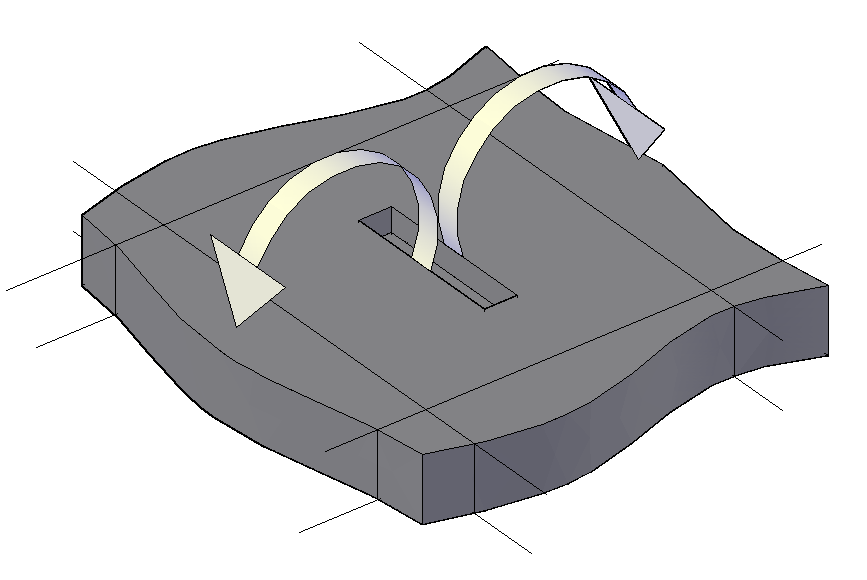
Rys. 2 Schemat obciążenia do wyznaczenia powierzchni wpływu dla maksymalnych momentów zginających
Możliwe jest również wyznaczenie powierzchni wpływu dla reakcji podporowych, sił tnących jak i innych wielkości. Sposób wyznaczania powierzchni wpływu przebiega jednakowo dla wszystkich typów stropów, czy to płytowo-słupowe, belkowe lub oparte na tarczach czy na ścianach.

Przykład wyznaczania powierzchni wpływu
Weźmy konkretny przykład. Stop płytowo-słupowy o 18-tu polach (rys. 3), rozpiętości przęseł zmienne od 3.0 m do 8.0 m, grubość płyty h = 0.20 m, wysokość kondygnacji H = 3.0 m, słupy kwadratowe o wymiarze boku b = 0.30 m. Podział płyty na elementy skończone (ES) pokazano na rys. 4. Materiał: beton C30/37.

Rys. 3 Geometria stropu i podział pól obciążenia
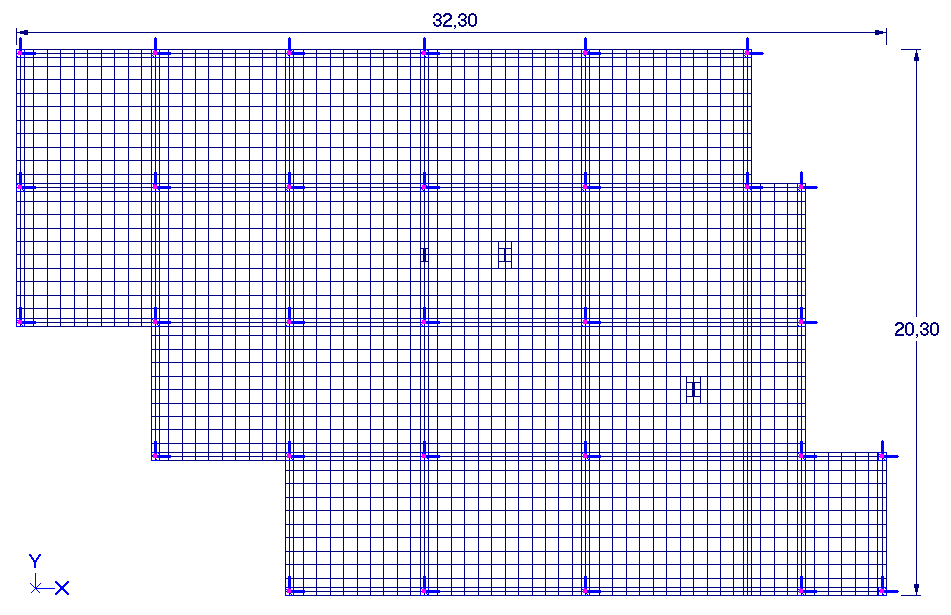
Rys. 4 Podział stropu na elementy skończone (3240 ES)
Powierzchnie wpływu będą wyznaczone dla czterech charakterystycznych miejsc stropu:
a) przęsło wewnętrzne,
b) przęsło skrajne,
c) w linii podpór (strefa w paśmie słupowym) oraz
d) podpora wewnętrzna.
W rezultacie otrzymamy obrazy powierzchni wpływowych dla analizowanego ustroju w odniesieniu do maksymalnych przemieszczeń (ugięć), momentów zginających oraz reakcji podporowych dla wybranych punktów. Na rys. 5 pokazałem przykładowy wynik bez obróbki dla powierzchni wpływu dla ugięcia w przęśle wewnętrznym (screen z programu ABC Płyta z zaznaczoną przyłożoną siłą).

Rys. 5a Obraz powierzchni wpływu dla ugięcia w przęśle wewnętrznym – obraz w rzucie
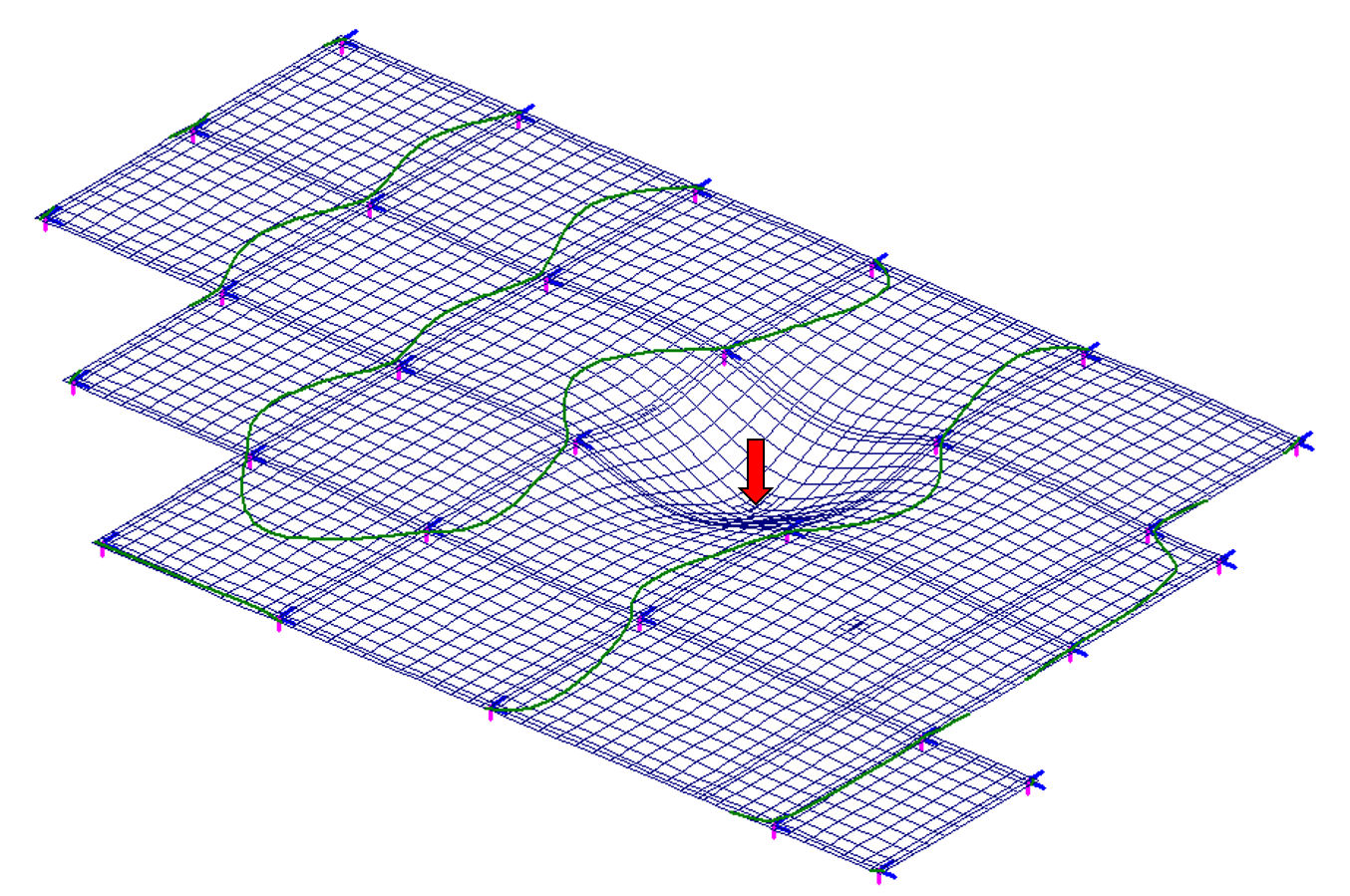
Rys. 5b Obraz powierzchni wpływu dla ugięcia w przęśle wewnętrznym – widok 3D
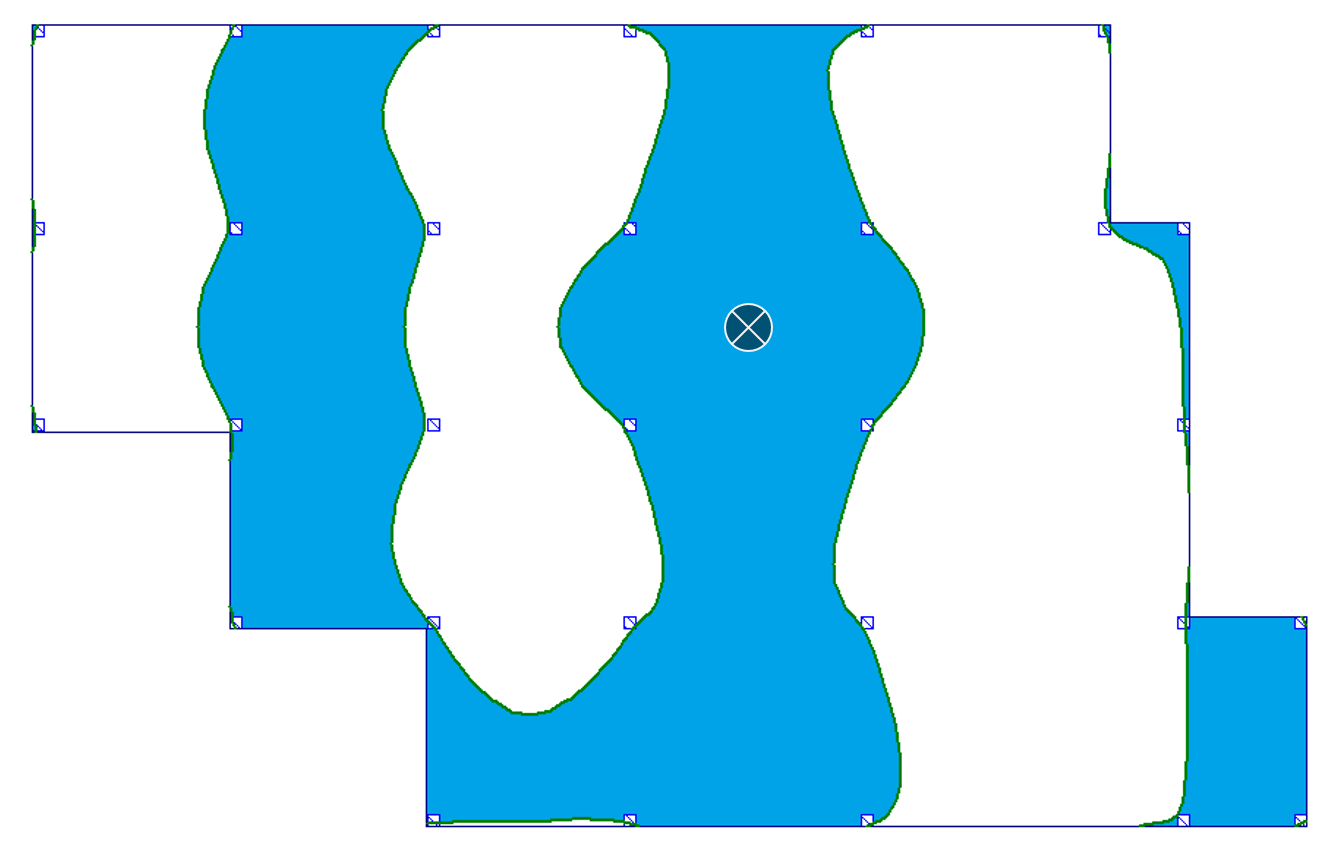
Poniżej w tabeli 1 zebrałem rysunki obrazujące przebieg granic powierzchni wpływu dla tych przypadków. (Strzałka na rysunkach przypisana jest dla momentów zginających, kółko dla ugięć.)
Tab. 1 Przebieg granic powierzchni wpływu dla wybranych miejsc
| Miejsce | Dla momentu zginającego | Dla ugięcia |
|---|---|---|
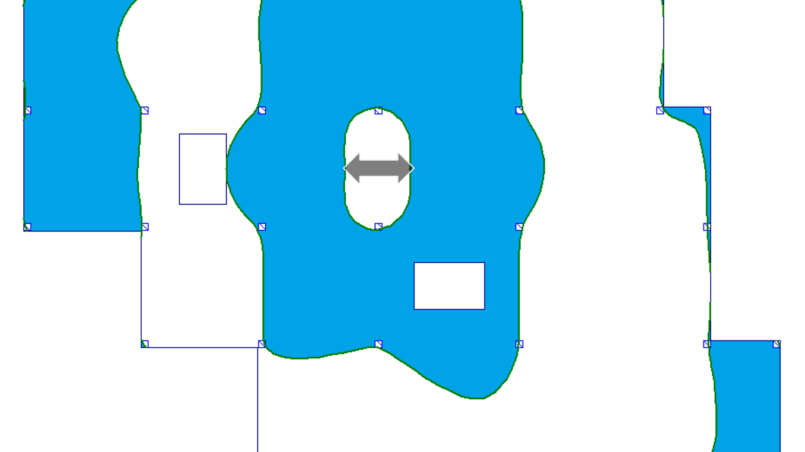
| a) przęsło wewnętrzne | 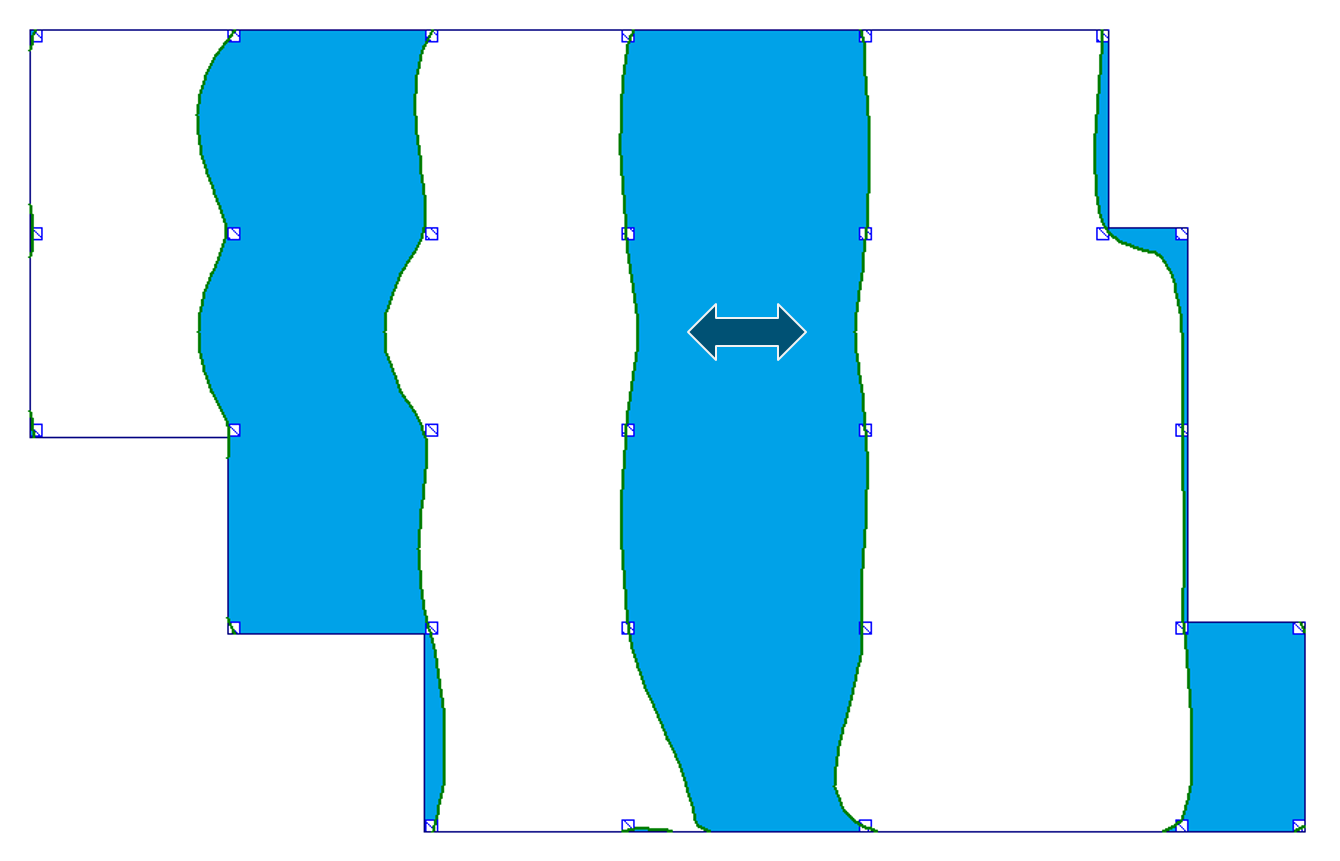 |
 |
| b) przęsło skrajne | 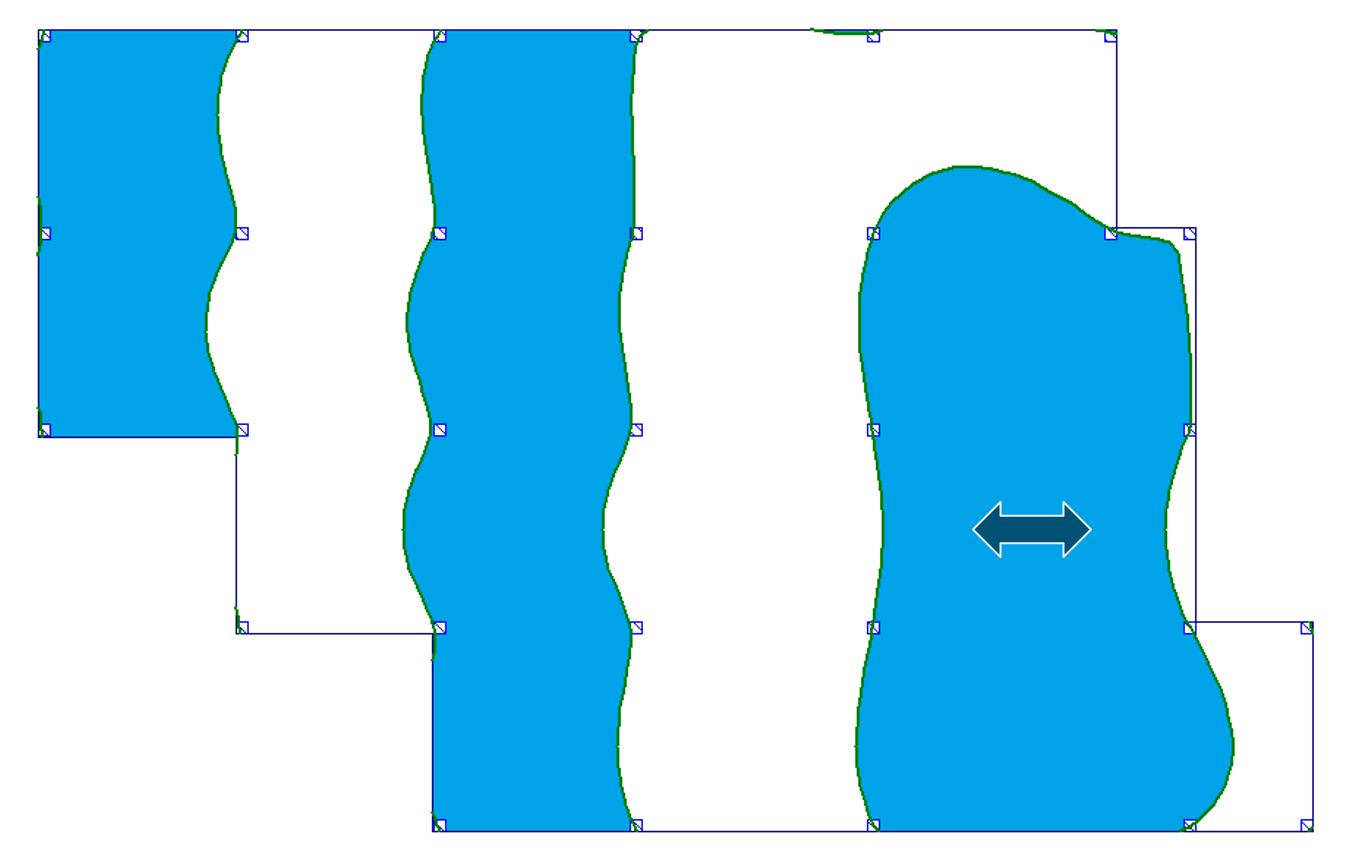 |
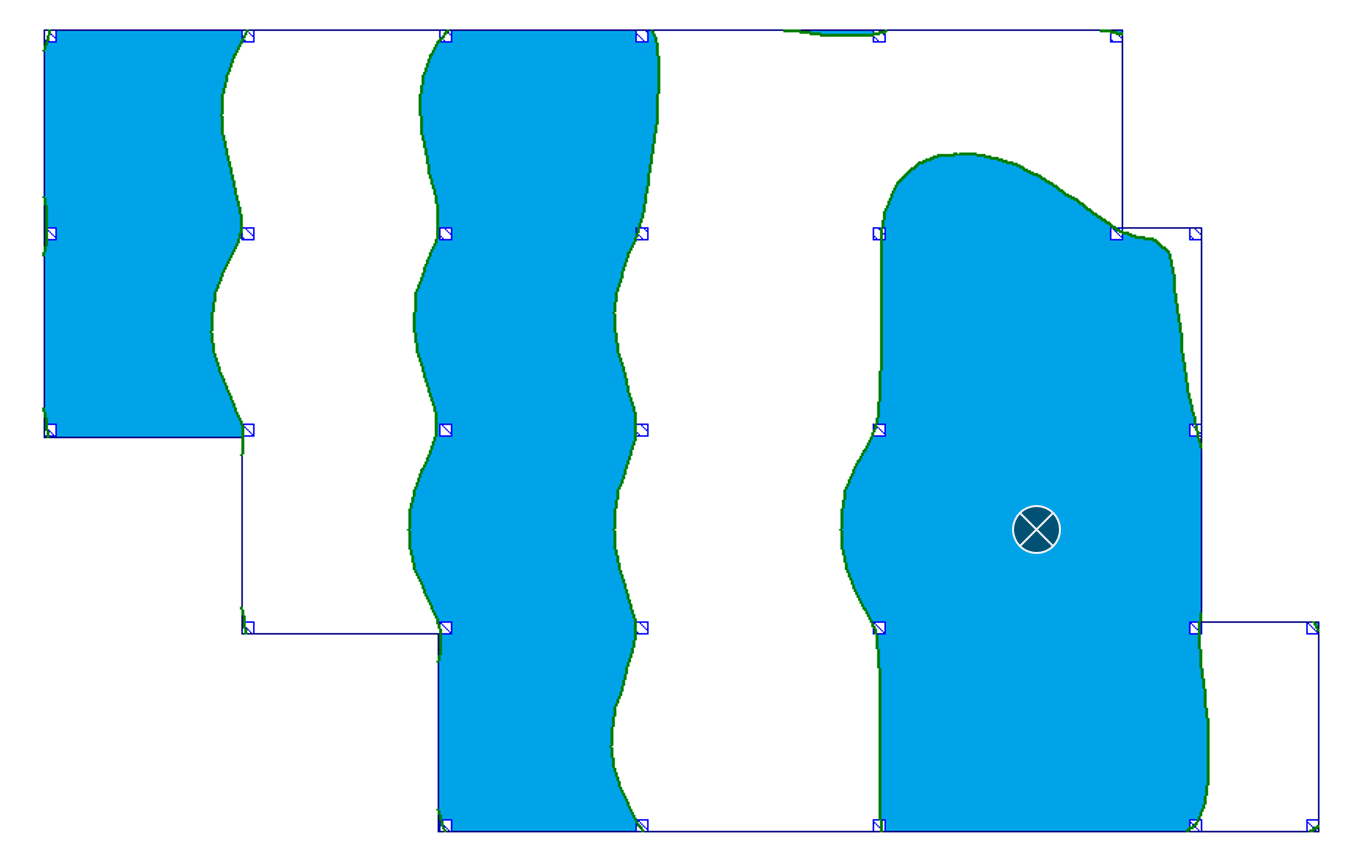 |
| c) w linii podpór | 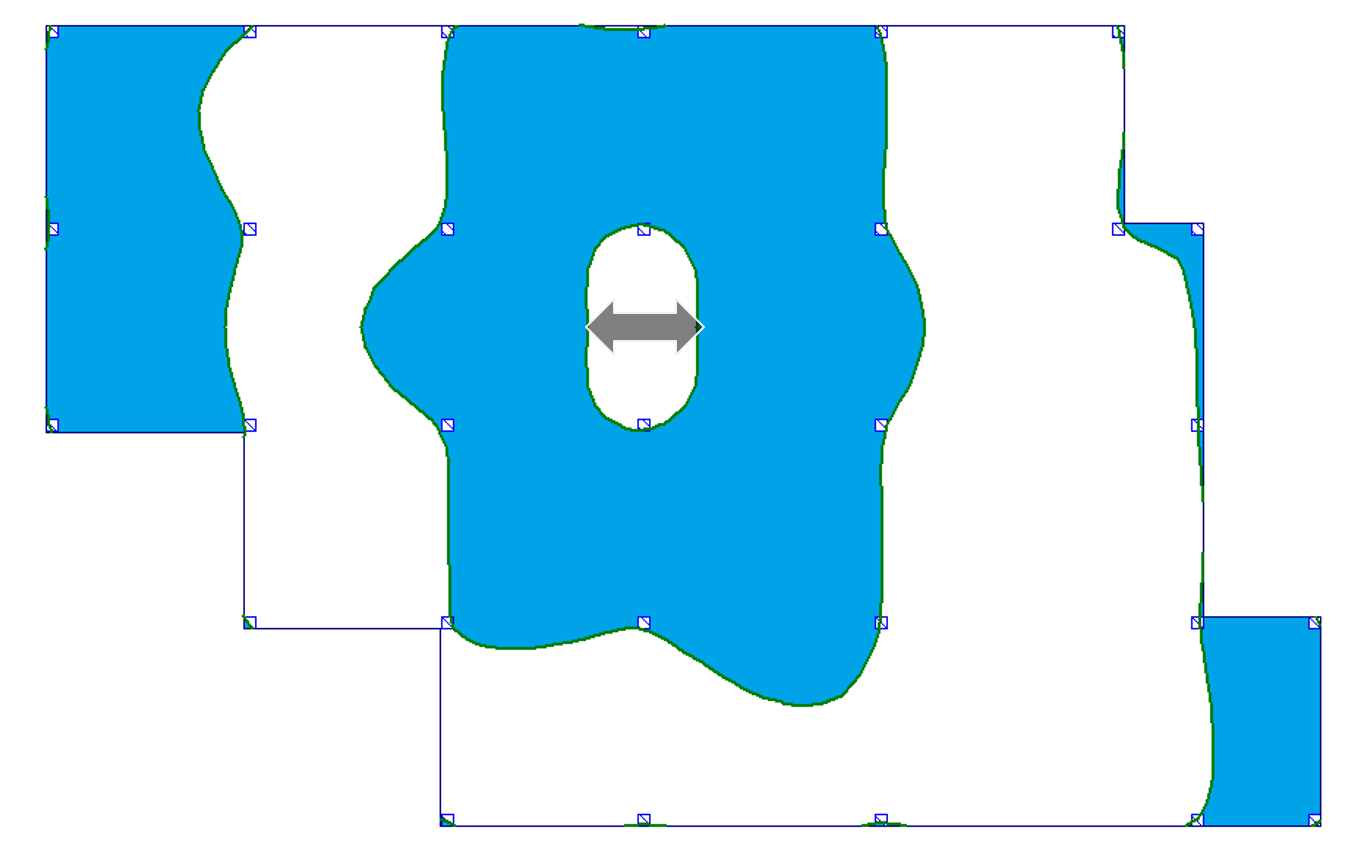 |
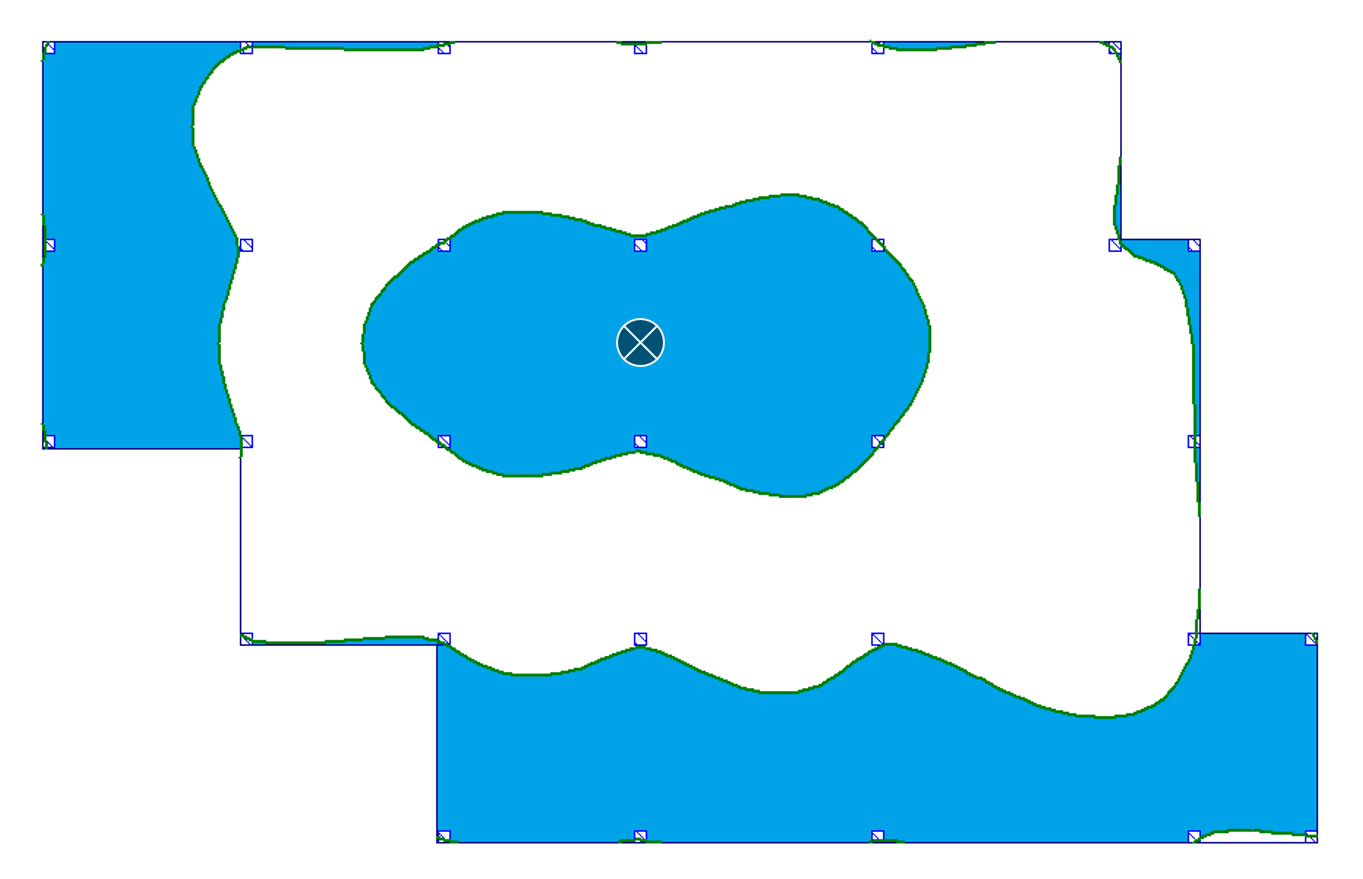 |
| d) podpora wewnętrzna (moment i reakcja podporowa) | 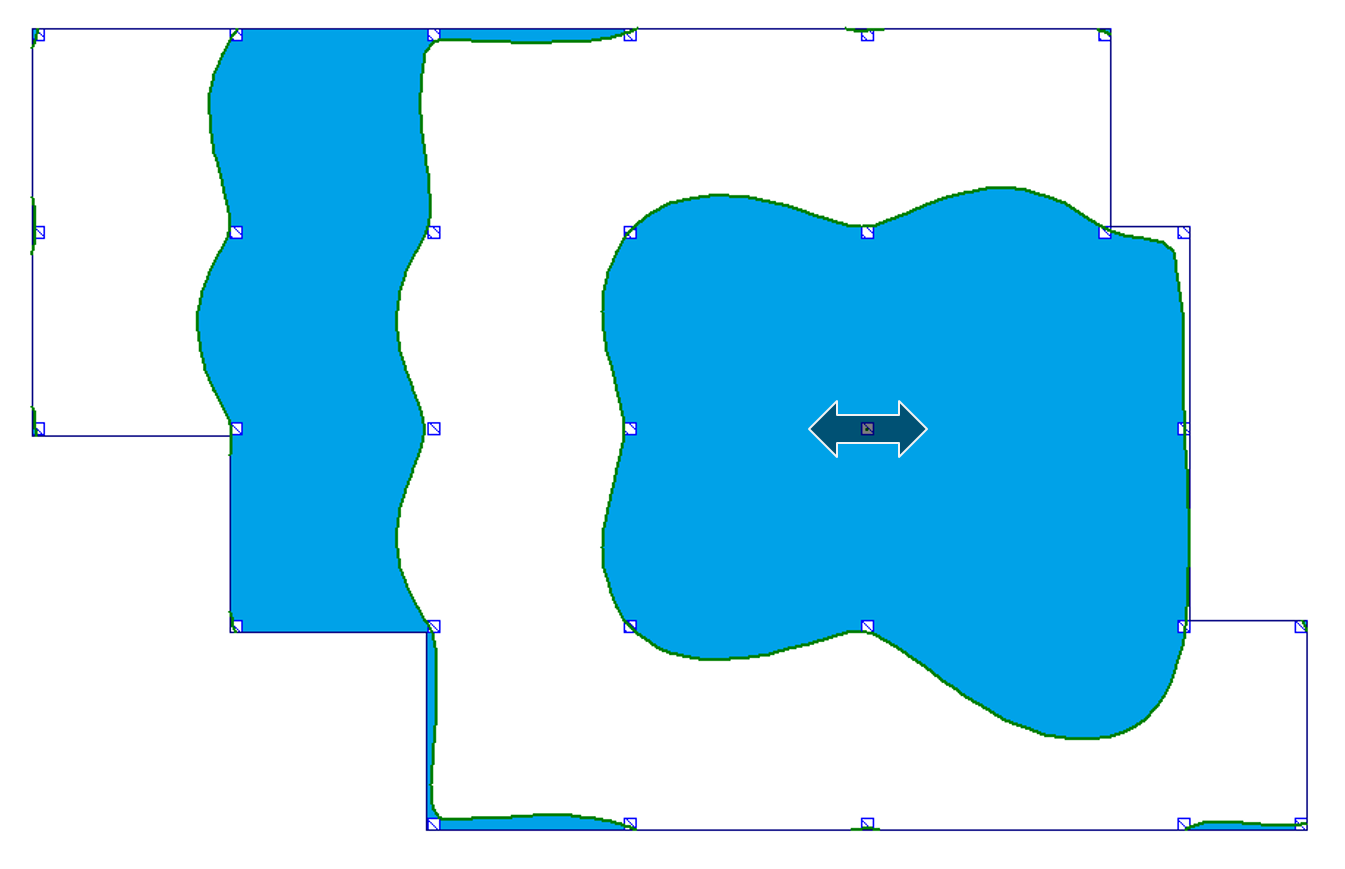 |
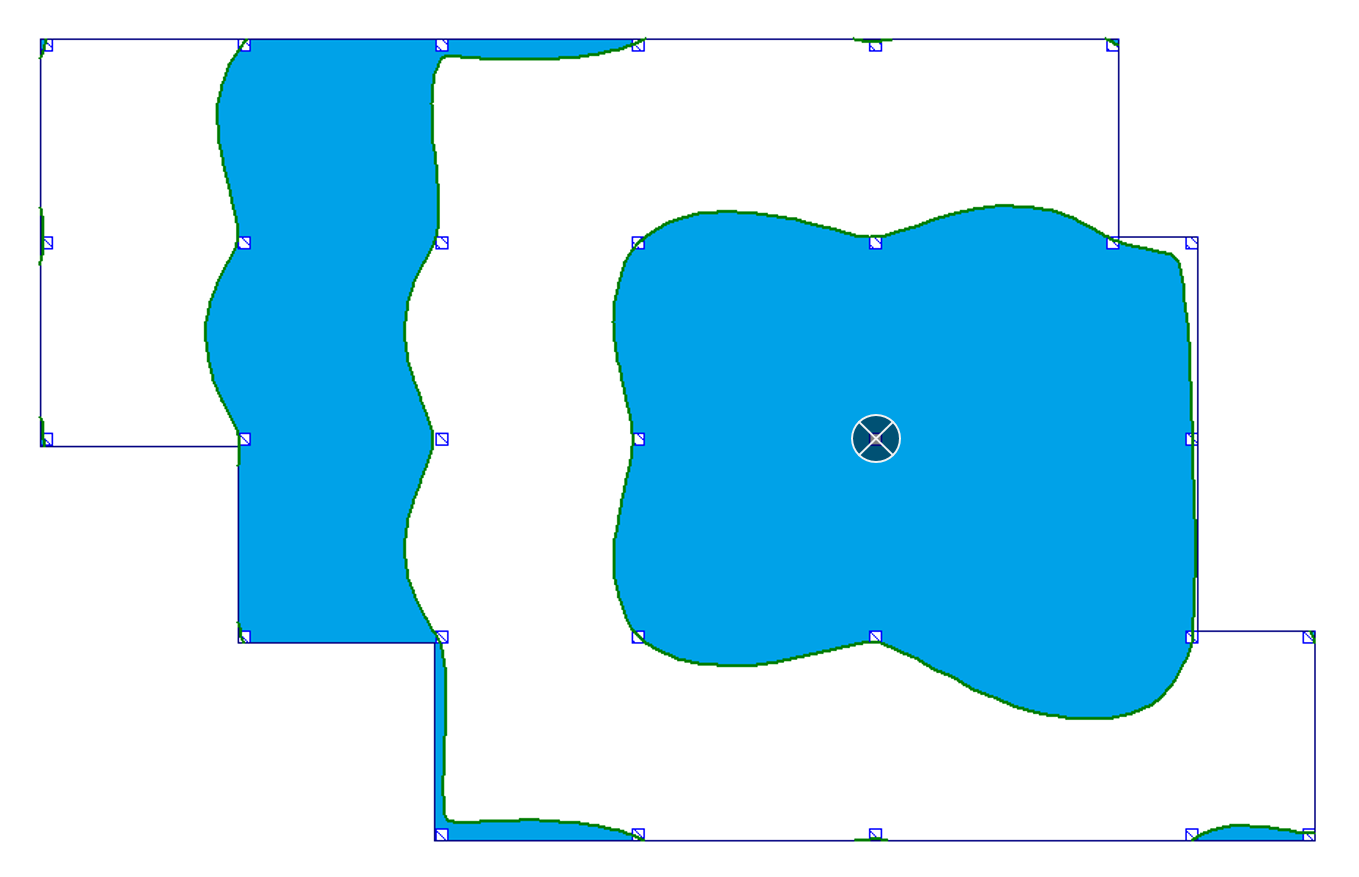 |
Na podstawie tych rysunków widać wyraźnie, że granice powierzchni wpływowych nie mają charakteru prostoliniowego. Krzywe wyznaczające granice nie mieszczą się również w obszarze poszczególnych pól – tj. pewne części pól, które wydawały się być „nieobciążone” dla uzyskania np. maksymalnego ugięcia – należałoby obciążyć, i odwrotnie. W przypadku gdy granice powierzchni wpływu przebiegających na niektórych polach nie obejmują całego obszaru tego pola, powstaje problem ewentualnego dzielenia obszaru obciążenia pól na mniejsze w przypadku obciążeń o stosunkowo dużych wartościach.
Jeszcze jedna sprawa. Chyba każdy strop posiada jakieś otwory – mniejsze lub większe? Powstaje pytanie, czy obecność otworów wpływa na kształt powierzchni wpływu? Sprawdźmy to na naszym przykładzie. Wprowadziłem dwa jednakowe, prostokątne otwory o wymiarach 2.0 x 3.0 m. Obrazy powierzchni wpływu zebrałem poniżej w tabeli 2.
Tab. 2 Przebieg granic powierzchni wpływu dla wybranych miejsc w stropie z otworami
| Miejsce | Dla momentu zginającego | Dla ugięcia |
|---|---|---|
| a) przęsło wewnętrzne | 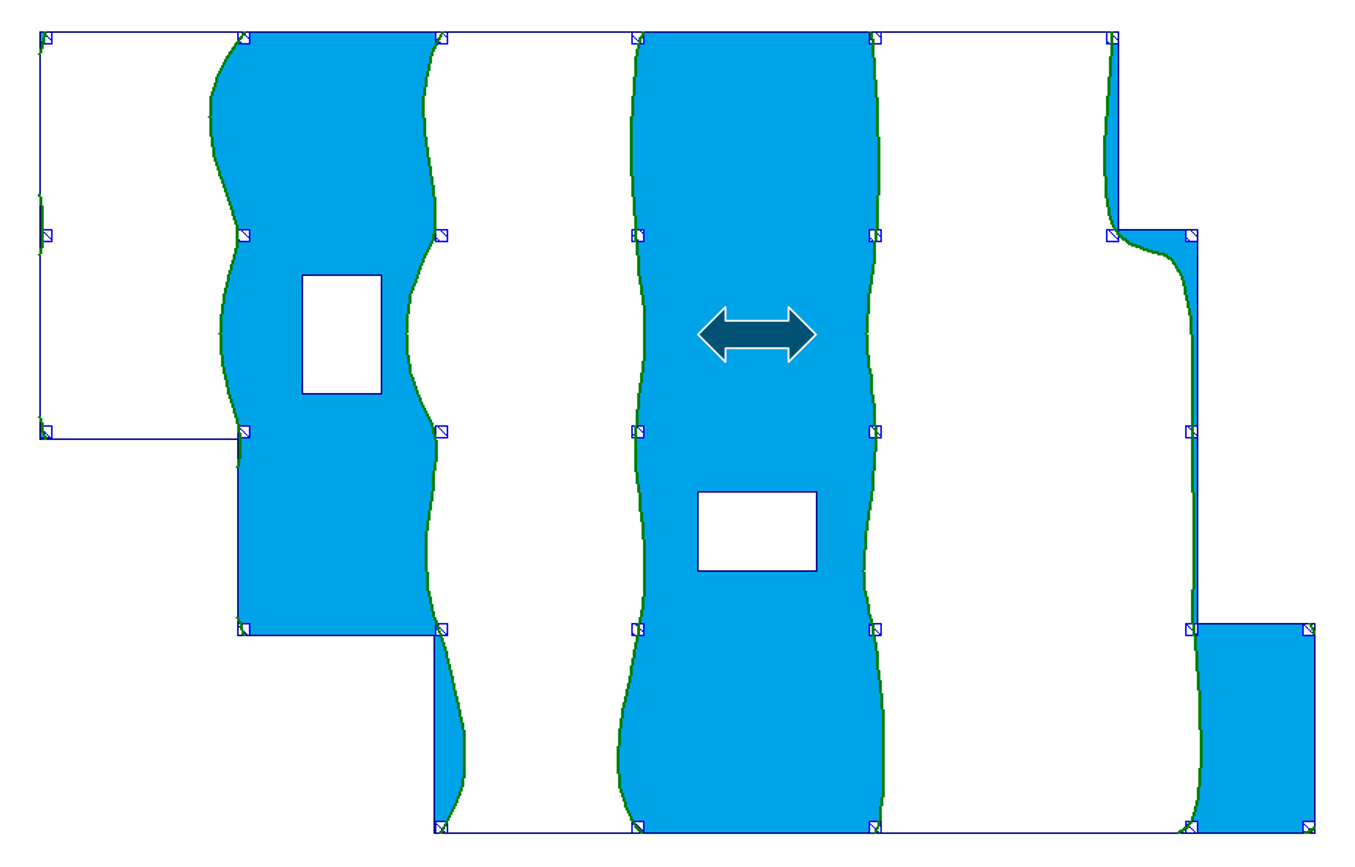 |
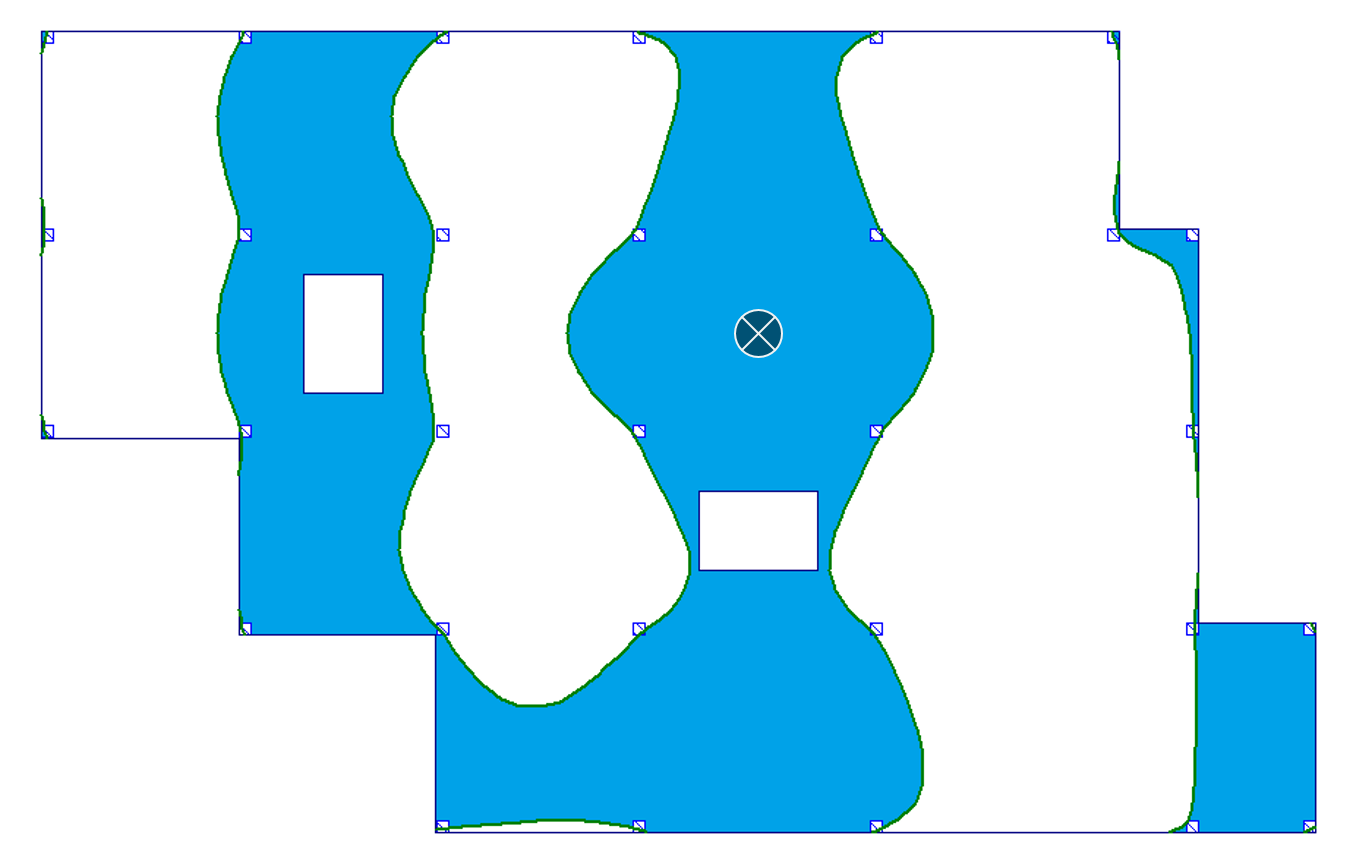 |
| b) przęsło skrajne | 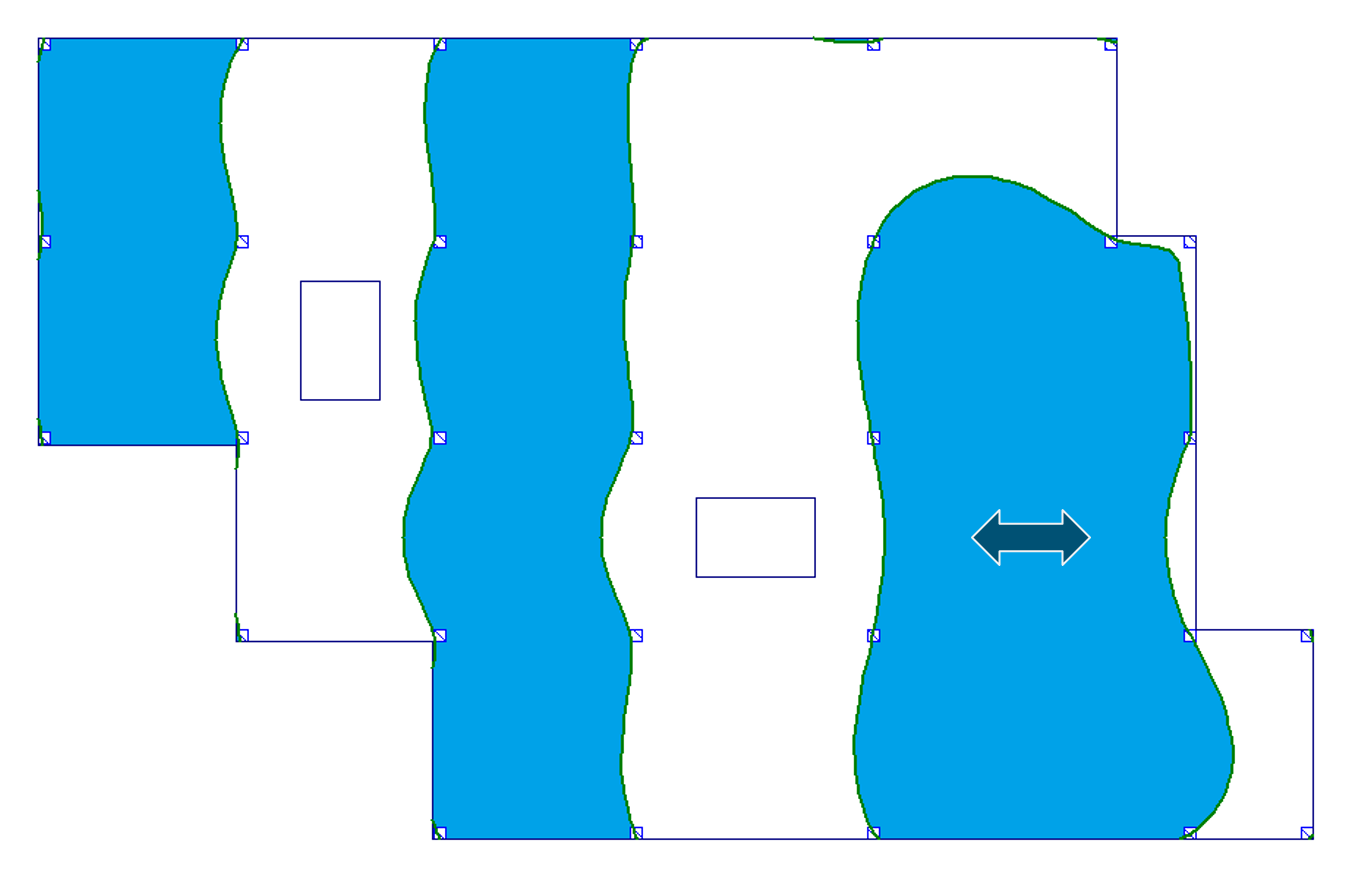 |
 |
| c) w linii podpór | 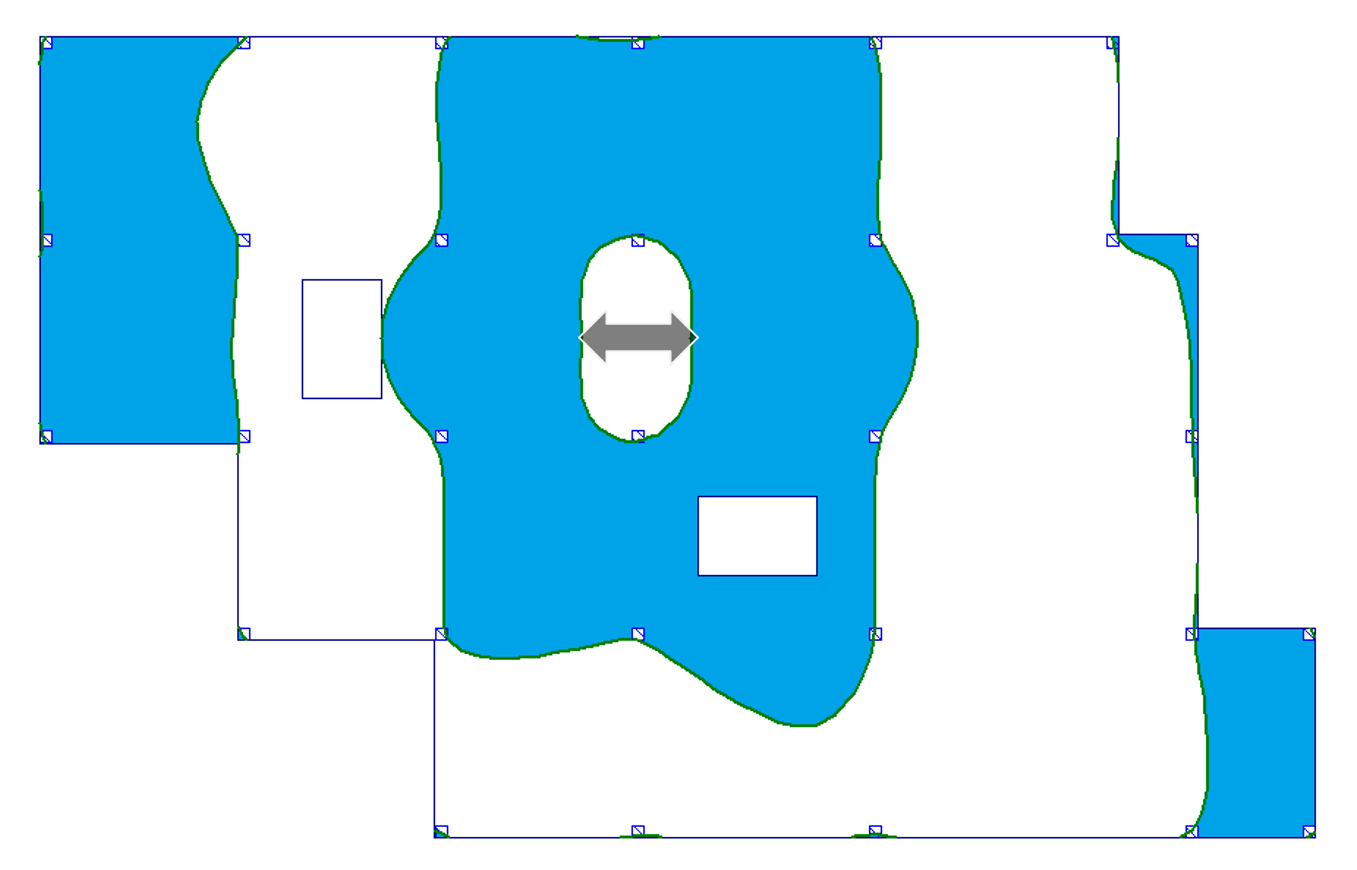 |
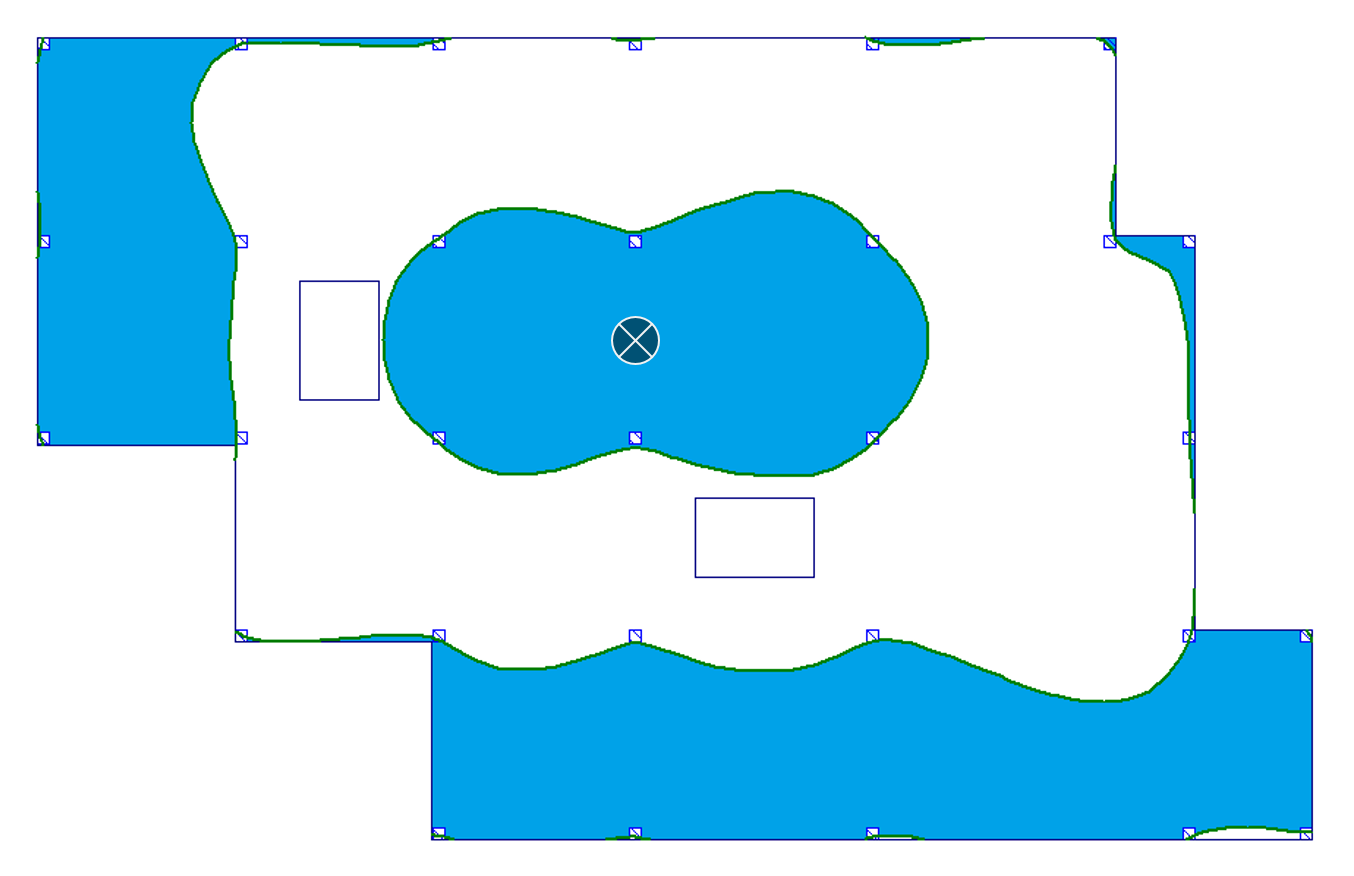 |
| d) podpora wewnętrzna (moment i reakcja podporowa) | 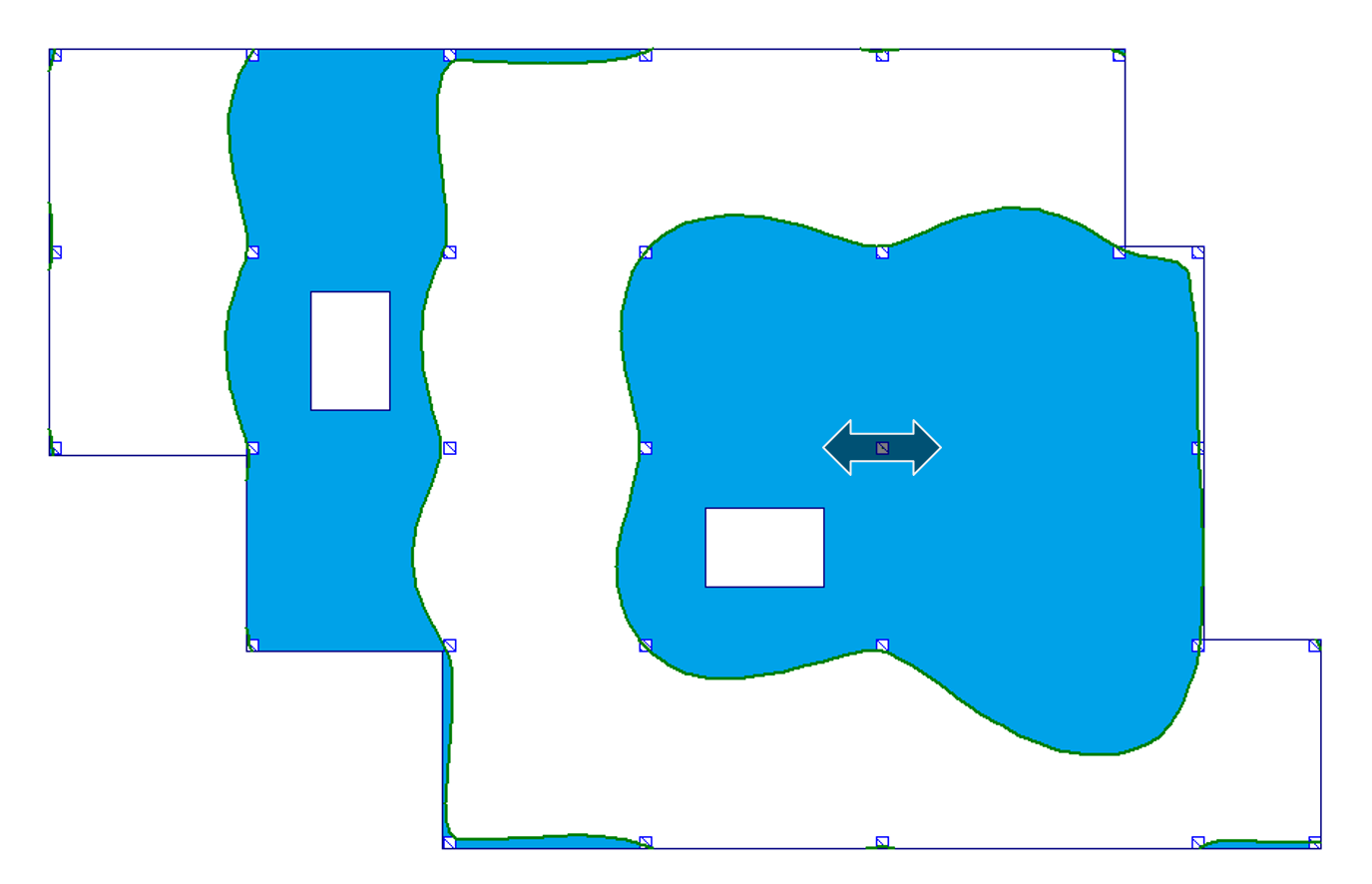 |
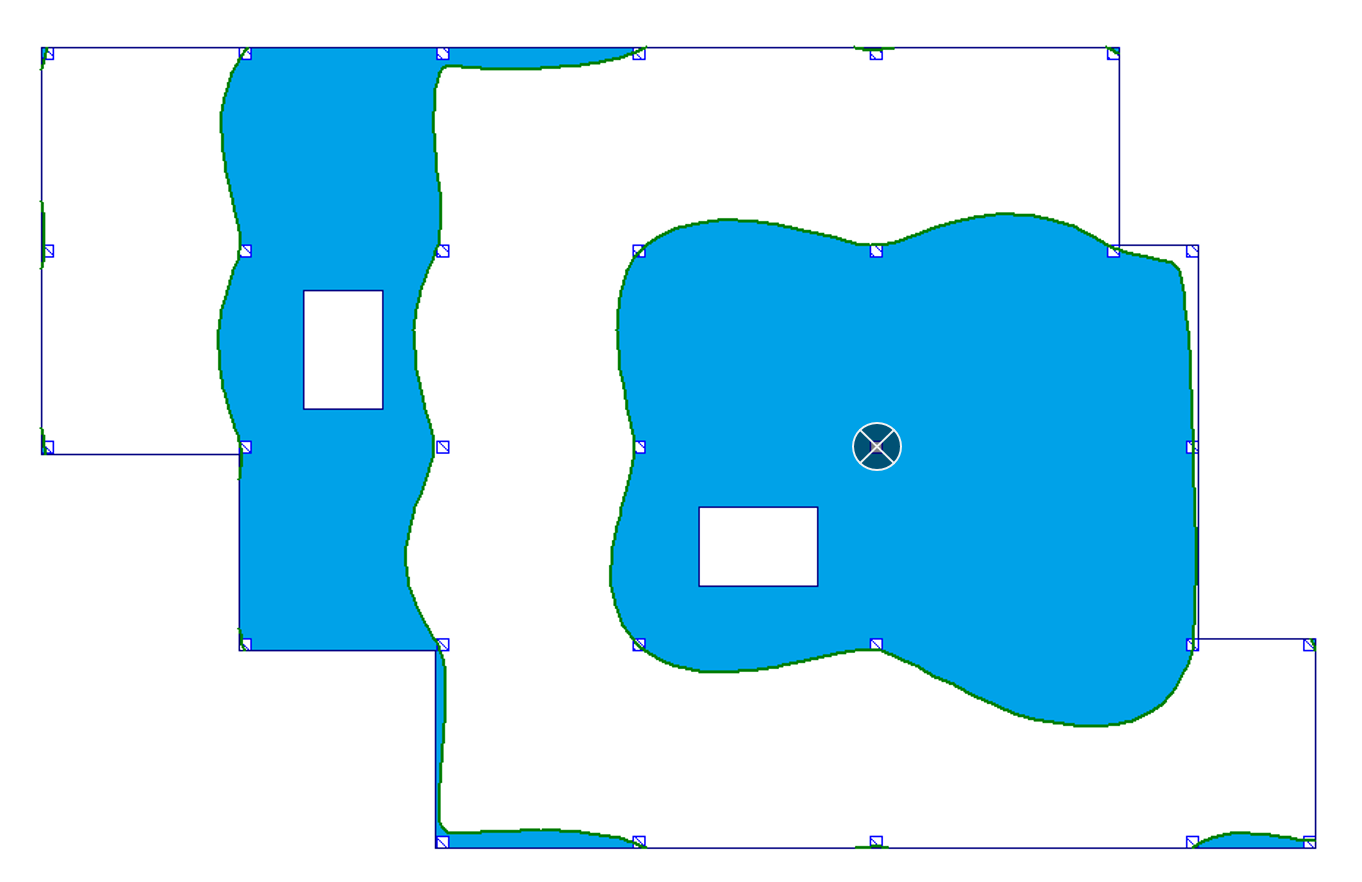 |
Jak możemy zobaczyć, powierzchnie wpływu dla stropu bez otworów i stropu z otworami są niemal identyczne. Niewielka różnica występuje jedynie w przypadku a) przęsło wewnętrzne dla wyników momentu zginającego (por. pole nr 16). Przy tak niewielkich różnicach możemy powiedzieć, że obecność otworów w płycie nie wpływa istotnie na przebieg granic powierzchni wpływu, poza fizycznym zniknięciem obszaru płyty w miejscach otworów.
Wnioski
Dowiedzieliśmy się w jaki sposób wyznaczać powierzchnie wpływu dla wybranych punktów, zarówno dla momentów zginających, ugięć i reakcji podporowych.
- Jak się okazuje granice powierzchni wpływu nie przebiegają liniowo wzdłuż osi podpór. Mają one raczej przebieg krzywoliniowy. Widać wyraźnie, że aby otrzymać najdokładniejszy rozkład obciążeń zmiennych i w konsekwencji dokładne wartości m.in. sił wewnętrznych i ugięć, należałoby rozkładać to obciążenie na podstawie obrazu powierzchni wpływu.
- W przypadku znacznej wartości obciążenia zmiennego należałoby się zastanowić nad ewentualnym podziałem pól na mniejsze. W niektórych przypadkach prowadziło by to do sytuacji, gdzie niektóre pola byłyby obciążone jedynie na części swojej powierzchni.
- Obecność zaburzeń w postaci otworów w płycie nie wpływa istotnie na przebieg granic powierzchni wpływu, wyłączając zanik tych powierzchni na obszarze otworu.
- Powierzchnie wpływu znajdują bezpośrednie zastosowanie w przypadkach, kiedy nie mamy pewności co do właściwego rozkładu obciążeń na stropie.
Post scriptum
Mam nadzieję, że tekst okazał się wam pomocny. Być może wyznaczanie powierzchni wpływu może wydawać się wam nieco abstrakcyjne, ale zobaczycie w kolejnych wpisach jak praktycznie z nich korzystać. Planuję pociągnąć dalej temat rozkładu obciążeń zmiennych dla różnych typów stropów.
Wpisy z cyklu „Rozkład obciążeń zmiennych„:
- Powierzchnie wpływu,
- Strop płytowo-słupowy,
- Strop płytowo-słupowy – metody alternatywne,
- Strop płytowo-belkowy,
- Strop oparty na ścianach (w opracowaniu).
Zapraszam do lektury! Jeśli macie pytania, komentujcie poniżej – obiecuję, że wszystkie przeczytam :)
Źródła
- Jastrzębski P., Mutermilch J., Orłowski W., Wytrzymałość materiałów, Cz.1, Arkady, Warszawa 1985,
- Starosolski W., Aneks do: Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, na prawach rękopisu, Pro-Soft, Gliwice 2007,
- Starosolski W., Komputerowe modelowanie betonowych ustrojów inżynierskich. Wybrane zagadnienia, t.1 i 2, Wyd. Politechniki Śląskiej, Gliwice 2009,
- Starosolski W., O rozmieszczeniu obciążeń zmiennych w stropach krzyżowo zbrojonych i płytowo-słupowych, Inżynieria i Budownictwo, nr 4/2008,
- Starosloski W., Projektowanie płytowo-słupowych ustrojów żelbetowych i sprężonych wg Euro-Norm, PRO-SOFT, Gliwice 2010,
- Starosolski W., Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, Wyd. Politechniki Śląskiej, Gliwice 2003,
- Zdanowicz Ł., Praca magisterska: Analiza obliczeniowa i projekt konstrukcji wielokondygnacyjnego budynku o ustroju płytowo-słupowym, Kraków 2010,
- PN-B-03264:2002 Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i projektowanie; w tekście jako PN02,
- PN-EN 1990:2004 Eurokod 0. Projektowanie konstrukcji z betonu. Cześć 1-1: Reguły ogólne i reguły dla budynków; w tekście jako EC0 lub Eurokod 0.