Jest wiele takich sytuacji, kiedy na element betonowy działa obciążenie skoncentrowane na niewielkiej powierzchni. Czasem może to być siła skupiona lub skoncentrowane obciążenie powierzchniowe.
Przykład: ściana żelbetowa podpierająca belkę lub inną ścianę powyżej, które biegną prostopadle do siebie. Rysunek poniżej obrazuje podane przez mnie przykłady.
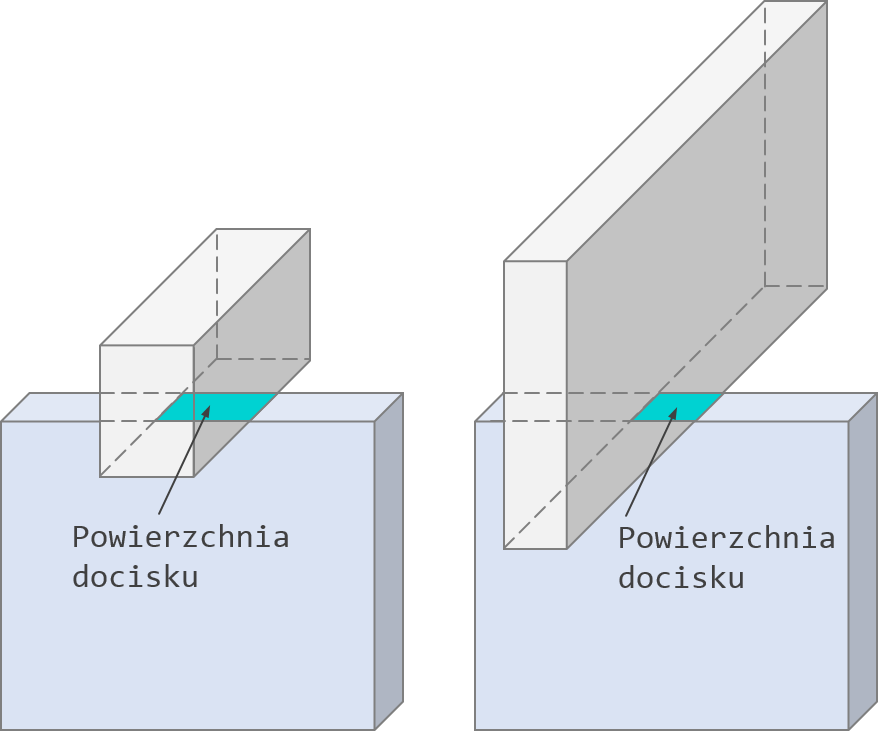
Rys. 1 Przykłady powierzchni poddanych działaniu obciążeń miejscowych
W takich przypadkach zachodzi ryzyko zniszczenia powierzchni na dwa sposoby:
- przez miejscowe miażdżenie betonu lub
- poprzeczne siły rozciągające.
W pierwszej sytuacji mamy do czynienia z typowym zjawiskiem docisku powierzchni betonowej. Należy sprawdzić obliczeniowo czy nośność betonu w tym miejscu jest wystarczająca. Mówi o tym Eurokod 2 (EC2) w punkcie 6.7.
Drugi punkt dotyczy ryzyka rozłupywania betonu pod powierzchnią docisku na skutek działania poprzecznych sił rozciągających. To zagadnienie jest opisane w Eurokodzie w pkt. 6.5
W tym wpisie zajmę się pierwszym zagadnieniem, czyli określeniem nośności na docisk powierzchni obciążonej miejscowo. Sposób wymiarowania zbrojenia na poprzeczne siły rozciągające opiszę w drugiej części tekstu dotyczącego docisku (link znajdziecie tutaj: Docisk, czyli jak projektować miejsca obciążone miejscowo – Cześć 2).
Nośność na docisk – równomierny rozkład obciążenia
W przypadku równomiernego rozkładu obciążenia na powierzchni docisku (patrz rys. 2) nośność można obliczać ze wzoru:
![Rendered by QuickLaTeX.com \[F_{Rdu} = A_{c0} \cdot f_{cd} \cdot \sqrt{\frac{A_{c1}}{A_{c0}}} \le 3 \cdot f_{cd} \cdot A_{c0}\]](https://oprojektowaniu.pl/wp-content/ql-cache/quicklatex.com-e8a21e072ce8c9c8cd719dd1c3da010a_l3.png)
gdzie: ![]() – powierzchnia docisku,
– powierzchnia docisku, ![]() – największa obliczeniowa powierzchnia rozdziału spełniająca wymagania rys. 2.
– największa obliczeniowa powierzchnia rozdziału spełniająca wymagania rys. 2.
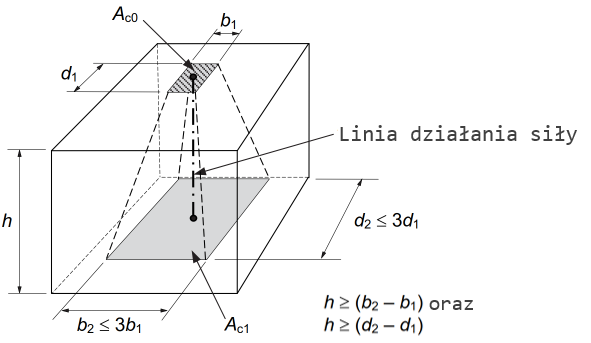
Rys. 2 Rozkład sił wywołany częściowym obciążeniem powierzchni [Fingerloos et al. 2016]
Jest jednak kilka warunków, które musi spełniać powierzchnia rozdziału ![]() , aby poprawnie określić nośność na docisk
, aby poprawnie określić nośność na docisk ![]() . Są to za Eurokodem 2:
. Są to za Eurokodem 2:
- wysokość, mierzona w kierunku obciążenia, na której pole przekroju ściskanego obszaru zwiększa się od
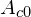 do
do 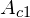 , powinna spełniać warunki podane na rys. 2,
, powinna spełniać warunki podane na rys. 2, - środek projektowanej powierzchni rozdziału
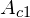 powinien znajdować się na linii działania przechodzącej przez środek powierzchni docisku
powinien znajdować się na linii działania przechodzącej przez środek powierzchni docisku 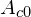 ,
, - przyjęta obliczeniowo powierzchnia rozdziału
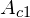 powinna mieć kształt podobny do
powinna mieć kształt podobny do 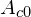 (
(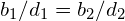 ),
), - jeżeli na przekrój betonu działa więcej niż jedna siła ściskająca, to zaprojektowane powierzchnie rozdziału nie powinny się nakładać.
Poniżej wyjaśnię dodatkowo co robić, kiedy warunki te nie są zachowane.
Nierównomierny rozkład obciążenia na powierzchni docisku
Co w przypadku, jeśli obciążenie nie jest równomierne rozłożone na powierzchni docisku ![]() ? Tutaj Eurokod 2 nie podaje rozwiązania, wspomina jedynie o konieczności redukcji wartości
? Tutaj Eurokod 2 nie podaje rozwiązania, wspomina jedynie o konieczności redukcji wartości ![]() . Podobnie jest w sytuacji, gdy mamy do czynienia z dużymi siłami ścinającymi.
. Podobnie jest w sytuacji, gdy mamy do czynienia z dużymi siłami ścinającymi.
Jednym ze sposobów na uwzględnienie nierównomiernego rozkładu obciążenia na powierzchni docisku jest odpowiednia redukcja tej powierzchni. Rysunek 3 wyjaśnia jak to zrobić.
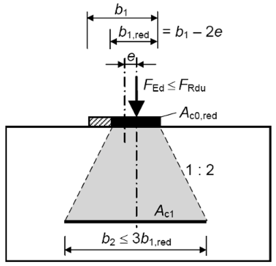
Rys. 3 Rozkład sił wywołany nierównomiernym obciążeniem powierzchni [Fingerloos et al. 2016]
Wynika z tego, że zamiast ![]() podstawiamy w obliczeniach zredukowaną wartość
podstawiamy w obliczeniach zredukowaną wartość ![]() (lub odpowiednio
(lub odpowiednio ![]() w miejsce
w miejsce ![]() ). W ten sposób otrzymujemy zredukowaną powierzchnię docisku
). W ten sposób otrzymujemy zredukowaną powierzchnię docisku ![]() i rozdziału
i rozdziału ![]() . Reszta obliczeń wygląda podobnie jak przy obciążeniu równomiernym.
. Reszta obliczeń wygląda podobnie jak przy obciążeniu równomiernym.

Nośność na docisk przy różnych powierzchniach docisku i rozdziału
Jeśli powierzchnia rozdziału ![]() nie jest podobna do powierzchnia docisku
nie jest podobna do powierzchnia docisku ![]() , czyli
, czyli ![]() , należy zmniejszyć wytrzymałość betonu.
, należy zmniejszyć wytrzymałość betonu.
Dla powierzchni obciążonej miejscowo, która zwiększa się tylko w jednym kierunku (dwuosiowy stan naprężenia, np. siła skupiona przyłożona na ścianę – por. rys. 4), maksymalne naprężenia w betonie powinny być ograniczone zgodnie z wzorem (6.60) w EC2 jak dla węzła ściskanego do wartości:
![]()
gdzie: ![]() – wartość przyjmowana wg pkt 6.5.4(4) EC2 (wartość zalecana przez EC2: 1.0),
– wartość przyjmowana wg pkt 6.5.4(4) EC2 (wartość zalecana przez EC2: 1.0), ![]() – współczynnik redukcji wytrzymałości betonu zarysowanego wg wzoru (6.57N) w EC2:
– współczynnik redukcji wytrzymałości betonu zarysowanego wg wzoru (6.57N) w EC2: ![]()
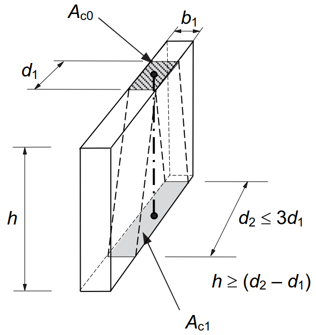
Rys. 4 Przykład rozkładu sił w przypadku różnych kształtów powierzchni docisku i rozdziału [Fingerloos et al. 2016]
W tym przypadku nośność na docisk będzie określana ze wzoru:
![]()
Nakładające się powierzchnie rozdziału
W przypadku występowania kilku powierzchni obciążonych miejscowo zlokalizowanych blisko siebie, gdzie powierzchnie rozdziału wyznaczone według rys. 2 nakładają się, należy ograniczyć wysokość ![]() , dla której określa się te powierzchnie, według rys. 5.
, dla której określa się te powierzchnie, według rys. 5.
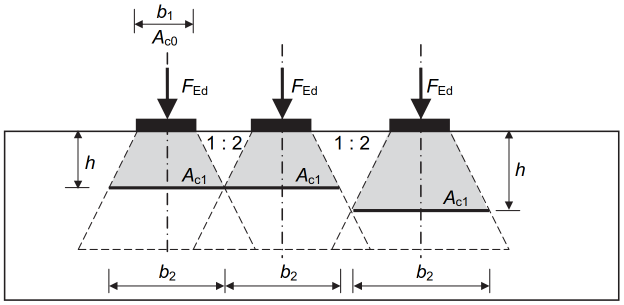
Rys. 5 Redukcja powierzchni rozdziału przy nakładających się obszarach rozkładu sił [Fingerloos et al. 2016]
Zwiększenie nośności na docisk
We wszystkich podanych wyżej przypadkach może zdarzyć się tak, że obciążenie, które działa na powierzchnię będzie większe niż nośność betonu na docisk (![]() ). Co wtedy zrobić?
). Co wtedy zrobić?
Generalnie, mamy kilka możliwości, m.in.:
- zwiększyć wytrzymałość betonu (podnieść klasę betonu),
- zwiększyć powierzchnię docisku (np. zwiększyć przekrój elementu) lub
- zastosować zbrojenie podłużne.
Skupię się tutaj na ostatnim punkcie, czyli dodaniu zbrojenia podłużnego w celu zwiększenia nośności na docisk. Zbrojenie to ma za zadnie przejąć różnicę pomiędzy przyłożonym obciążeniem a nośnością betonu, czyli ![]() .
.
Wymagane obliczeniowo zbrojenie ![]() ze względu na warunek nośności na docisk określa się ze wzoru:
ze względu na warunek nośności na docisk określa się ze wzoru:
![]()
Zbrojenie na poprzeczne siły rozciągające
Dla każdego z podanych przypadków należy dodatkowo zastosować odpowiednie zbrojenie na siły rozciągające spowodowane obciążeniem miejscowym. O tym piszę w Części 2, gdzie podaję procedurę na wymiarowanie zbrojenia poprzecznego.
W przypadku, kiedy takiego zbrojenia nie zastosowano, nośność na docisk należy zredukować według poniższego wzoru:
![]()
Przykład obliczeniowy
Weźmy za przykład belkę opartą na ścianie (rys. 6). Wymiary przekroju poprzecznego belki: 25/45 cm, grubość ściany: 25 cm. Klasa betonu obu elementów: C30/37. Reakcja do przeniesienia z belki na ścianę przez obciążoną powierzchnię wynosi ![]() .
.
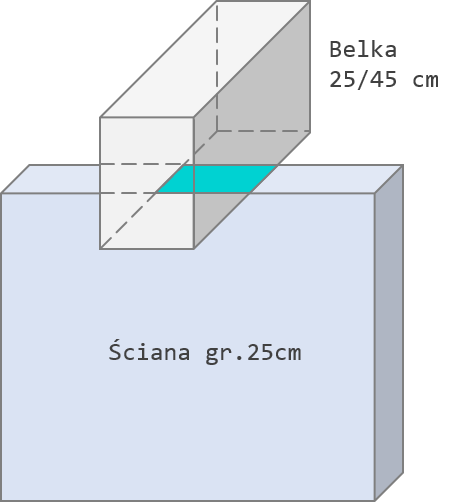
Rys. 6 Przykład obliczeniowy – podciąg oparty na ścianie
Tok obliczeń:
![]()
![]()
![]()
![]()
(W tym przypadku nie ma potrzeby wyznaczania powierzchni rozdziału ![]() .)
.)
![]()
Warunek na nośność betonu przy docisku nie jest spełniony: ![]()
Wyznaczenie wymaganego obliczeniowo zbrojenia: ![]()
![]()
Przyjęto dodatkowe zbrojenie podłużne: 4#12 (![]() ) oraz dodatkowe zbrojenie poprzeczne ().
) oraz dodatkowe zbrojenie poprzeczne ().
Ciąg dalszy nastąpi…
Drugą część tekstu dotyczącą docisku i wymiarowania zbrojenia na poprzeczne siły rozciągające znajdziecie TUTAJ.
Źródła
- Eurokod 2: PN-EN 1992-1-1, Projektowanie konstrukcji z betonu. Część 1-1: Reguły ogólne i reguły dla budynków
- Fingerloos F., Hegger J., Zilch K., EUROCODE 2 für Deutschland – Kommentar, Ernst & Sohn / Beuth, 2016
- PN-B-03264:2002, Konstrukcje betonowe, żelbetowe i sprężone – Obliczenia statyczne i projektowanie
- Albert A. et al., Schneider – Bautabellen für Ingenieure, Bundesanzieger Verlag, 2016
- Vismann U. et al., Wendehorst Bautechnische Zahlentafeln, Springer / Beuth, 2015
Z pozdrowieniami





Cześć! Brakuje mi tutaj wyjaśnienia skąd wziąć wartość h. Na przykładowych rysunkach widać, że można wyznaczyć ją prowadząc linię skośną 1:2, jest to jednak wyciąg z literatury. A gdzie szukać wytycznych normowych? Jest rysunek, jest wymiar h, są podane pewne ograniczenia, ale jak obliczyć wartość h nie podano.
Dlaczego nie ma potrzeby wyznaczania Ac1? Przecież pierwiastek z dzielenia Ac1/Ac0, przez który mnożymy iloczyn Ac*fcd mógłby nam sporo zwiększyć wytrzymałość na docisk. Swoją drogą, przed przystąpieniem do lektury intuicyjnie myślałem, że taka wytrzymałość będzie mniejsza niż zwykła wytrzymałość na ściskanie.
Przykład obliczeniowym dotyczy belki opartej na ścianie. Powierzchnia docisku jest geometrycznie inna niż powierzchnia rozdziału, wobec czego nie spełnia wymagania b1/d1 = b2/d2, które podałem na początku tekstu (zobacz w artykule: NOŚNOŚĆ NA DOCISK – RÓWNOMIERNY ROZKŁAD OBCIĄŻENIA). W takim przypadku należy zredukować nośność na docisk wg akapitu NOŚNOŚĆ NA DOCISK PRZY RÓŻNYCH POWIERZCHNIACH DOCISKU I ROZDZIAŁU.
Obliczeniowo wszystko jest możliwe, ale nie wszystko jest poprawne ;) Trzeba uważać z jakim przypadkiem ma się do czynienia.
Wytrzymałość betonu w złożonym stanie naprężenia (np. trójosiowe ściskanie) jest większa od maksymalnych naprężeń ściskających w jednej płaszczyźnie czy osi. To tak jak ze skrępowaniem betonu.
Ach, to przez to, że miałem problem z algorytmem tego zagadnienia i wyznaczaniem powierzchni docisku. Zastanawiałem się na przykład gdzie jest płaszczyzna, w której leży ta powierzchnia ;) Już wszystko jasne. To, jak bardzo możemy oddalać od siebie A0 i A1 zależy od podanych ograniczeń. W treści artykułu nie było to wystarczająco zaakcentowane, a przykład był trochę za prosty, żeby rozwiać wątpliwości.
Że papier przyjmie wszystko zdaję sobie sprawę, ale z drugiej strony ten wzór nie wygląda mi na wyprowadzony z teorii sprężystości, to by był zresztą temat na inny, a nawet trochę więcej innych artykułów (Edit: z drugiego komentarza doczytałem, że jest to model s-t). Dzięki za odpowiedź i pozdrawiam!
Dzięki Krzysztof za feedback! Przykład obliczeniowy dotyczy jednej z najczęściej spotykanych sytuacji w projektowaniu. Zachęcam do samodzielnego przerobienia też innych przypadków :)
Gratuluję bardzo udanego artykułu! Temat jest bardzo ważny, ponieważ znane są z historii przypadki i kłopotów wynikających z nieadekwatnego zazbrojenia ścian opartych na sobie punktowo (jak w przykładzie). Eurokod 2 jest bardzo oszczędny jeśli chodzi o zasady obliczania powierzchni obciążonych miejscowo, w przeciwieństwie do „starej normy”, gdzie zagadnienie to było omówione bardzo obszernie.
Bardzo cenię spotykane często w EC2 określenia „powinno się”, „należy uwzględnić”, „należy zastosować”, itp. – bez wskazania, w jaki sposób należy to zrobić ;-). W tym miejscu ukłony dla Autora, który podjął się próby wyjaśnienia zawiłości normy.
A na marginesie głos w dyskusji – norma nakazuje, by w przypadku elementów obciążonych w przybliżeniu osiowo maksymalne skrócenie nie przekraczało 2‰ – w przypadku stali o granicy plastyczności powyżej 400MPa pojawia się problem, ponieważ w ujęciu obliczeniowym nie można w pełni wykorzystać jej parametrów wytrzymałościowych. Problem dotyczy nie tylko słupów, ale również ścian – jak w przykładzie. Chciałem zapytać, jak zapatruje się na to Autor :-).
Pozdrowienia z Łodzi
Dziękuję Michał za ciekawy komentarz. „Naszą starą” normę PN-B-03264 znam i na boku zerkałem do niej :) Nie chciałem jawnie się na nią powoływać, żeby nie robić zamieszania.
Co do Twojego pytania o wykorzystania nośności zbrojenia przy granicznych odkształceniach betonu, to bardzo ciekawe pytanie! Tutaj można sporo dyskutować, ale pozwól, że dam przykład rachunkowy. Załóżmy, że obciążenie powierzchni wywołuje graniczne odkształcenie w betonie na poziomie wspomnianych przez Ciebie 2‰. Wtedy w zbrojeniu – o ile występuje – mamy naprężenia rzędu sigma.s = epsilon * Es = 0.002 * 200 GPa = 400 MPa (zakładam równość odkształceń). Mamy zatem tutaj poziom granicy plastyczności. Problem pojawia się – tak jak wspomniałeś – przy stali o wyższej granicy plastyczności, wtedy stal – wg tego podejścia – nie jest w pełni wykorzystywana…
Tutaj tylko przypomnę, że model, na którym oparty jest algorytm docisku, bazuje na modelu 'strut and tie’, który bazuje na naprężeniach nieliniowych a nie na odkształceniach. Rzeczywistość jest bardziej zawiła ;) W pokazanym tutaj przykładzie nie ma jawnego uwzględnienia pola zbrojenia (lub tzw. przekroju sprowadzonego), a przecież m.in. od ilości pola zbrojenia i betonu zależy rozdział działającej siły na beton i stal. W ogólnym przypadku należało zamiast wyznaczać zbrojenie na podstawie deltaFEd należałoby (jak to lubi EC2 :)) od początku liczyć nośność betonu i stali na całą siłę FEd.
Nie wiem czy rozjaśniłem coś moim komentarzem, ale wkład do dyskusji dałeś pierwszorzędny! :) W procedurach projektowych jest właśnie tak, że im dłużej się im przygląda, tym więcej pytań się pojawia ;)